B Standard normal probability distribution

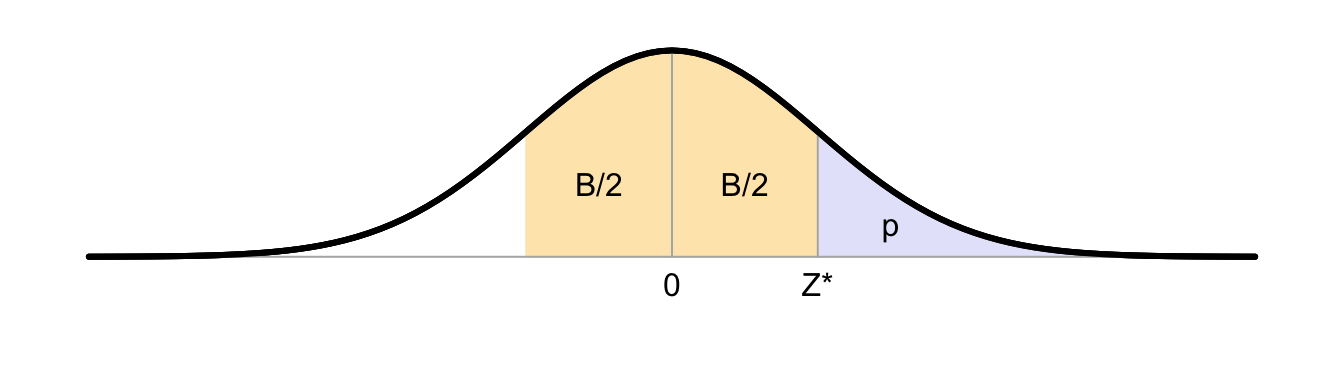
The critical value \(Z^*\) given below has a probability of \(p\) under \(H_0\), i.e., \(P(Z > Z^*|H_0)=p\) (the blue area), and it has a probability of \(B\) to have a value in the interval \((-Z^*, +Z^*)\) (the yellow area). The \(Z\) distribution is symmetrical around \(Z=0\), hence \(P(Z < -Z^*) = P(Z > Z^*)\).

---

The first table reports the critical boundary values \(Z^*\) for some frequently used probabilities of \(p\) and frequently used confidence intervals of \(B\):

p	0.2	0.1	0.05	0.025	0.01	0.005	0.0025	0.001
B	60%	80%	90%	95%	98%	99%	99.5%	99.8%
Z*	0.8416	1.282	1.645	1.960	2.326	2.576	2.807	3.090

---

The second table reports the probabilities \(p\) and confidence intervals \(B\) for some frequently used critical values of \(Z^*\):

p	0.3085	0.1587	0.0668	0.0228	0.0062	0.0013	0.0002
B	38.29%	68.27%	86.64%	95.45%	98.76%	99.73%	99.95%
Z*	0.5	1	1.5	2	2.5	3	3.5