C Critical values for \(t\)-distribution

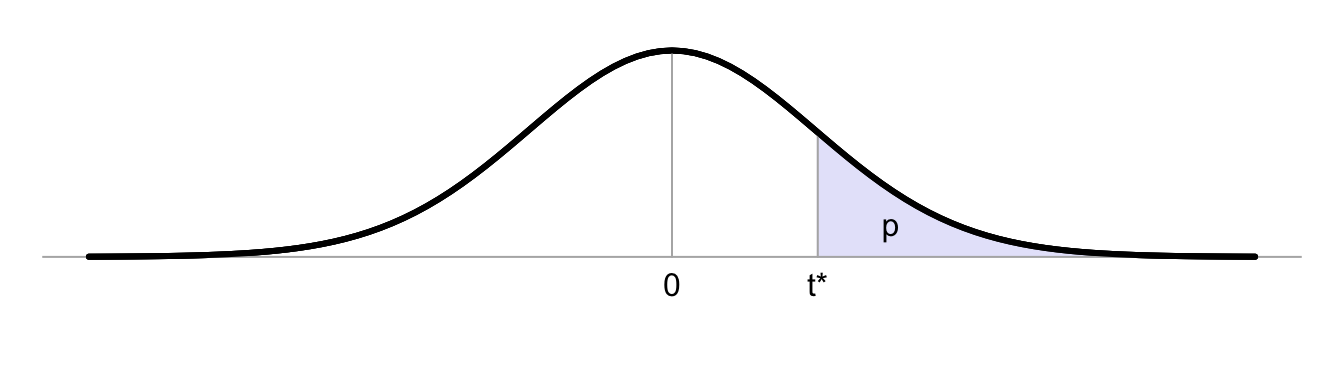
The critical boundary value \(t^*\) given below has a critical probability \(p\) under \(H_0\), i.e. \(P(t \geq t^*|H_0)=p\), and has probability \(B\) of a value between \((-t^*, +t^*)\). The \(t\)-distribution is symmetric around \(t=0\), thus \(P(t < -t^*) = P(t > t^*)\).

The table below provides the critical boundary values \(t^*\) for much used critical probabilities \(p\) and confidence intervals \(B\), for the degrees of freedom indicated in the first column.

	p	0.2	0.1	0.05	0.025	0.01	0.005	0.0025	0.001
	B	60%	80%	90%	95%	98%	99%	99.5%	99.8%
1		1.376	3.078	6.314	12.706	31.821	63.657	127.321	318.309
2		1.061	1.886	2.920	4.303	6.965	9.925	14.089	22.327
3		0.9785	1.638	2.353	3.182	4.541	5.841	7.453	10.215
4		0.941	1.533	2.132	2.776	3.747	4.604	5.598	7.173
5		0.9195	1.476	2.015	2.571	3.365	4.032	4.773	5.893
6		0.9057	1.440	1.943	2.447	3.143	3.707	4.317	5.208
7		0.896	1.415	1.895	2.365	2.998	3.499	4.029	4.785
8		0.8889	1.397	1.860	2.306	2.896	3.355	3.833	4.501
9		0.8834	1.383	1.833	2.262	2.821	3.250	3.690	4.297
10		0.8791	1.372	1.812	2.228	2.764	3.169	3.581	4.144
11		0.8755	1.363	1.796	2.201	2.718	3.106	3.497	4.025
12		0.8726	1.356	1.782	2.179	2.681	3.055	3.428	3.930
13		0.8702	1.350	1.771	2.160	2.650	3.012	3.372	3.852
14		0.8681	1.345	1.761	2.145	2.624	2.977	3.326	3.787
15		0.8662	1.341	1.753	2.131	2.602	2.947	3.286	3.733
16		0.8647	1.337	1.746	2.120	2.583	2.921	3.252	3.686
17		0.8633	1.333	1.740	2.110	2.567	2.898	3.222	3.646
18		0.862	1.330	1.734	2.101	2.552	2.878	3.197	3.610
19		0.861	1.328	1.729	2.093	2.539	2.861	3.174	3.579
20		0.860	1.325	1.725	2.086	2.528	2.845	3.153	3.552
21		0.8591	1.323	1.721	2.080	2.518	2.831	3.135	3.527
22		0.8583	1.321	1.717	2.074	2.508	2.819	3.119	3.505
23		0.8575	1.319	1.714	2.069	2.500	2.807	3.104	3.485
24		0.8569	1.318	1.711	2.064	2.492	2.797	3.091	3.467
25		0.8562	1.316	1.708	2.060	2.485	2.787	3.078	3.450
30		0.8538	1.310	1.697	2.042	2.457	2.750	3.030	3.385
40		0.8507	1.303	1.684	2.021	2.423	2.704	2.971	3.307
50		0.8489	1.299	1.676	2.009	2.403	2.678	2.937	3.261
100		0.8452	1.290	1.660	1.984	2.364	2.626	2.871	3.174
200		0.8434	1.286	1.653	1.972	2.345	2.601	2.839	3.131
400		0.8425	1.284	1.649	1.966	2.336	2.588	2.823	3.111
∞		0.8416	1.282	1.645	1.960	2.326	2.576	2.807	3.090