Hoofdstuk 8 Frequenties
8.1 Inleiding
Bij de analyse van gegevens wordt vaak een onderscheid gemaakt tussen kwalitatieve danwel kwantitatieve methoden. Bij de eerste methode worden waarnemingen (bijv. antwoorden in interviews) gerepresenteerd in woorden, en bij de tweede methode worden waarnemingen (bijv. spreekpauzes in interviews) gerepresenteerd in getallen. Naar onze mening bestaat het verschil tussen kwalitatieve en kwantitatieve methoden dus uit de aard van de representatie van de observaties, en daarmee uit de wijze van argumentatie op grond van die observaties. Soms is het ook mogelijk om dezelfde gegevens (bijv. interviews) zowel kwalitatief als kwantitatief te analyseren. De kwantitatieve methode heeft als grote voordelen dat de gegevens relatief eenvoudig samengevat kunnen worden (daarover gaat dit deel van het tekstboek), en dat het relatief makkelijk is om zinvolle conclusies te trekken op basis van de observaties.
8.2 Frequenties
Kwantitatieve gegevens kunnen op allerlei manieren gerapporteerd worden. De eenvoudigste manier zou zijn om de ruwe gegevens te rapporteren, bij voorkeur gesorteerd naar de waarde van de geobserveerde variabele. Nadeel daarvan is dat een eventueel patroon in de observaties niet goed zichtbaar wordt.
Voorbeeld 8.1: Studenten \((N=50)\) in een eerstejaars cursus rapporteerden de volgende waarden voor hun schoenmaat, een variabele van het interval-meetniveau:
36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 38, 38, 38, 38, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 40, 40, 40, 40, 40, 40, 41, 41, 41, 41, 41, 42, 42, 43, 43, 44, ??.
Eén van de studenten heeft geen antwoord opgegeven; dit ontbrekende antwoord is hier aangegeven als ??.
Meestal is het inzichtelijker en efficiënter om de observaties samen te vatten en te rapporteren in de vorm van de frequentie van elke waarde. Die frequentie geeft het aantal observaties met een bepaalde waarde, of met een waarde in een bepaald interval of klasse. Om de frequentie te verkrijgen tellen we dus het aantal observaties met een bepaalde waarde, of het aantal observaties in een bepaald interval. Deze frequenties worden gerapporteerd in een tabel. Zo’n tabel wordt een frequentieverdeling genoemd (frequency distribution).
Tabel 8.1 geeft als eerste voorbeeld een frequentieverdeling van een discrete variabele van nominaal meetniveau, nl. de fonologische klasse van spraakklanken in het Nederlands (Luyckx et al. 2007).
| hoofdklasse | onderklasse | aantal |
|---|---|---|
| C | plos | 585999 |
| C | fric | 426097 |
| C | liq | 249275 |
| C | nas | 361742 |
| C | glide | 146344 |
| V | lang | 365887 |
| V | kort | 428832 |
| V | schwa | 341260 |
| V | diph | 61638 |
| V | rest | 1146 |
Tabel 8.2 geeft als tweede voorbeeld een frequentieverdeling van een continue variabele van interval meetniveau, nl. de al eerder genoemde schoenmaat van eerstejaars studenten (Voorbeeld 8.1).
| Schoenmaat | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | ?? |
| Aantal | 2 | 6 | 6 | 19 | 6 | 5 | 2 | 2 | 1 | 1 |
Als een numerieke variabele heel veel verschillende waarden kan aannemen, dan wordt de frequentieverdeling op deze manier toch groot en onoverzichtelijk. We voegen dan waarden in een bepaald interval bij elkaar, en maken daarna een frequentieverdeling over dat geringere aantal intervallen of klassen.
Voorbeeld 8.2: Toen Koningin Beatrix voor het laatst de Troonrede voorlas, op 18 september 2012, pauzeerde ze daarbij \(305\times\). De frequentieverdeling van de duur van de pauze (gemeten in seconden) is weergegeven in Tabel 8.3.
| Interval | Aantal |
|---|---|
| 4.50–4.99 | 1 |
| 4.00–4.49 | 0 |
| 3.50–3.99 | 2 |
| 3.00–3.49 | 7 |
| 2.50–2.99 | 4 |
| 2.00–2.49 | 25 |
| 1.50–1.99 | 32 |
| 1.00–1.49 | 16 |
| 0.50–0.99 | 67 |
| 0.00–0.49 | 151 |
8.2.1 Intervallen
Voor een variabele van nominaal en ordinaal meetniveau gebruiken we doorgaans de oorspronkelijke categorieën om de frequentieverdeling te maken (zie Tabel 8.1), al is het wel mogelijk om categorieën samen te voegen. Voor een variabele van interval- of ratio-meetniveau kan een onderzoeker zelf het aantal intervallen in de frequentieverdeling kiezen. Soms is dat niet nodig, bijvoorbeeld omdat de variabele een overzichtelijk aantal verschillende discrete waarden heeft (zie Tabel 8.2). Maar soms sta je als onderzoeker voor de keuze hoeveel intervallen te onderscheiden, en hoe de grenzen van die intervallen te bepalen (zie Tabel 8.3). Daarbij gelden dan de volgende aanbevelingen (Ferguson and Takane 1989, Ch.2):
Zorg dat alle observaties (d.w.z. het gehele bereik) vallen binnen ruwweg 10 tot 20 intervallen.
Zorg dat alle intervallen even breed zijn.
Laat de ondergrens van het eerste of tweede interval samenvallen met de breedte van de intervallen (zie Tabel 8.3: ieder interval is 0.50 s breed, en de ondergrens van het tweede interval is ook 0.50).
Orden de intervallen in een frequentieverdeling van beneden naar boven in toenemende volgorde (d.i. van boven naar beneden in afnemende volgorde, Eng. descending), zie Tabel 8.3).
Naarmate we de intervallen breder maken, verliezen we meer informatie over de precieze verdeling binnen elk interval.
8.2.2 SPSS
Analyze > Descriptive Statistics > Frequencies...Selecteer variabele (sleep naar paneel “Variable(s)”).
Vink aan: Display frequency tables.
Kies Format, kies: Order by: Descending values.
Bevestig met OK.
8.2.3 JASP
Klik in de bovenbalk op Descriptives. Selecteer vervolgens de gewenste variabele(n) en plaats ze in het veld “Variables”. Vink Frequency tables (nominal and ordinal variables) (onder het veld met alle variabelen) aan om voor alle geselecteerde variabelen van nominaal en ordinaal meetniveau een frequentietabel als uitvoer te krijgen.
Mocht een variabele als meetniveau “Scale” hebben en je wilt hiervan een frequentietabel, dan moet je eerst het meetniveau aanpassen naar “Nominal” of “Ordinal” door in het data tabblad op het meetniveau-icoontje voor de naam van de variabele te klikken.
Een variabele van interval of ratio meetniveau kan ook eerst worden opgedeeld in een aantal intervallen. Dit doe je door een nieuwe variabele aan te maken waarbij de originele scores worden omgezet in een interval. Maak de nieuwe variabele aan door op de +-button te klikken rechts van de naam van de laatste kolom in de dataset. Er verschijnt een paneel “Create Computed Column”, waar je een naam voor de nieuwe variabele kunt invullen, bijvoorbeeld troon12_interval. Ook kun je kiezen uit R en een aanwijshandje. Dit zijn de twee opties in JASP om formules te definiëren waarmee de nieuwe (lege) variabele wordt gevuld; met R code of handmatig. Hieronder wordt voor allebei de opties uitgelegd hoe we hiermee de variabele met intervallen maken. Als laatste kun je aanvinken welk meetniveau de variabele moet krijgen; dat is in dit geval “Ordinal”. Klik vervolgens op Create Column om de nieuwe variabele aan te maken. De nieuwe variabele (kolom) verschijnt als meest rechtse in de data en is nog leeg.
Als R is aangeklikt als optie om de nieuwe variabele te definiëren, verschijnt er boven de data een veld met “#Enter your R code here :)”. Hier kan R code worden gegeven die met behulp van R functies de nieuwe variabele definieert. Vul de R code in en klik onderaan op Compute column om de lege variabele te vullen met de gekozen waardes.
Om de variabele ‘troon2012’ op te delen zoals in Tabel 8.3 kan de volgende code worden gebruikt:
cut(troon2012, breaks = seq(0, 5, 0.5)) Hiermee worden de duren van de spreekpauzes van Koningin Beatrix in de Troonrede van 2012 opgedeeld in intervallen van halve seconden (0.5 = breedte interval), en alle intervallen samen lopen van 0 (ondergrens eerste interval) tot 5 (bovengrens laatste interval) seconden. Als je niet precies de breedte en het totale bereik van de intervallen wil bepalen, maar een x aantal gelijke intervallen wilt, kan de volgende code worden gebruikt:
cut(troon2012, 10) Hiermee worden de scores opgedeeld in 10 even brede intervallen, waarbij de ondergrens van het eerste interval gelijk is aan de laagste score die er was, en de bovengrens van het laatste interval is gelijk aan de hoogste score die er was.
Als het aanwijshandje is aangeklikt als optie om de nieuwe variabele te definiëren, verschijnt er boven de data een veld met links daarvan de variabelen, boven wiskundige symbolen, en rechts een aantal functies. Hier kan handmatig de functie worden geselecteerd die de nieuwe variabele definieert. Klik onderaan op Compute column om de lege variabele vervolgens te vullen met de gekozen waardes.
Om een variabele op te delen in een aantal gelijke intervallen selecteer je rechts de functie cut(y). Sleep de variabele die je wilt opdelen naar “values” en typ het aantal intervallen dat je wilt op de plek van “numBreaks”. Om zelf de breedte en het totale bereik van de intervallen te bepalen zul je de R code optie moeten gebruiken (hierboven beschreven).
Voor de nieuwe variabele opgedeeld in intervallen kan de frequentietabel worden verkregen zoals helemaal bovenaan beschreven. Ga naar Descriptives, selecteer de gewenste variabele (troon12_interval) in het veld “Variables” en vink Frequency tables (nominal and ordinal variables) (onder het veld met alle variabelen) aan.
8.2.4 R
enq2011 <- read.table(
file=url("http://www.hugoquene.nl/R/enq2011.txt"),
header=TRUE )
table( enq2011$schoen, useNA="ifany" ) De uitvoer van bovenstaande table commando is weergegeven in Tabel 8.2.
De code NA (Not Available) wordt in R gebruikt om ontbrekende gegevens aan te duiden.
# lees dataset
load(file="data/pauses6.Rda")
# haal daaruit pauzeduren (kolom 12) voor jaar 2012, in aparte variabele `troon2012`
troon2012 <- pauses6[ pauses6$jaar==2012, 12 ] # save col_12 as single vectorOntleed bovenstaande opdracht vanuit de binnenste haakjes naar buiten:
(i) seq: maak een reeks (sequence) van 0 tot 5 (eenheden, hier: seconden) in stappen van 0.5 seconden,
(ii) cut: hak de afhankelijke variabele troon2012 (duren van pauzes in de Troonrede van 2012) op in intervallen op basis van deze reeks,
(iii) table: maak een frequentieverdeling van deze intervallen.
De uitvoer van deze laatste opdracht is weergegeven (in aangepaste vorm) in Tabel 8.3, en wordt hier onderdrukt.
8.3 Staafdiagrammen
Een staafdiagram (Eng. ‘bar chart’) is de grafische weergave van de frequentieverdeling van een discrete, categorische variabele (van nominaal of ordinaal meetniveau). Een staafdiagram is opgebouwd uit rechthoeken. Alle rechthoeken zijn even breed, en de hoogte van de rechthoek correspondeert met de frequentie van die categorie. De oppervlakte van iedere rechthoek correspondeert dus ook met de frequentie van die categorie. In tegenstelling tot een histogram sluiten de rechthoeken niet op elkaar aan langs de horizontale as, om aan te geven dat we te maken hebben met discrete categorieën.
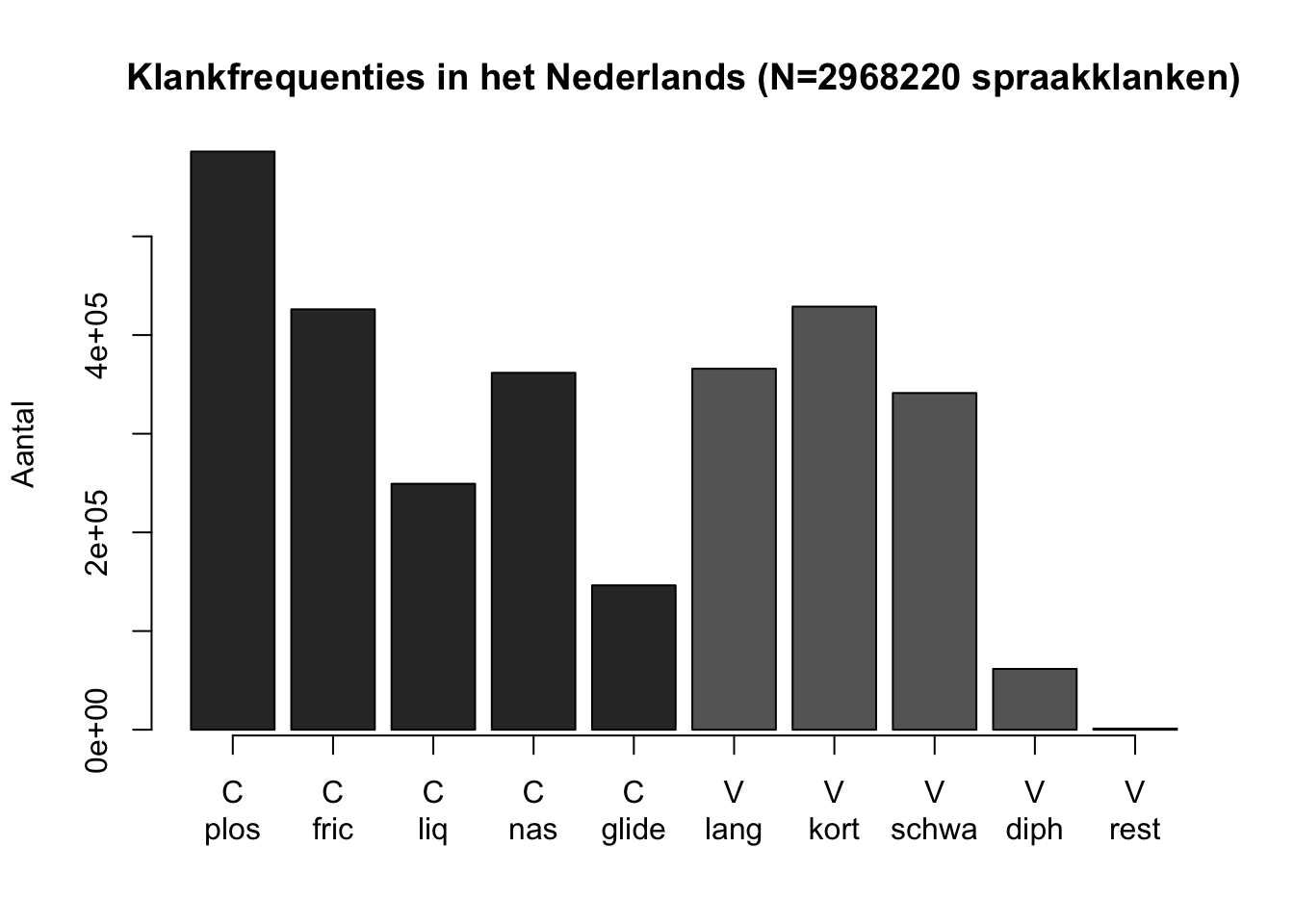
Figuur 8.1: Staafdiagram van de frequentieverdeling van fonologische klasse van spraakklanken in het Corpus Gesproken Nederlands (C=consonant=medeklinker, V=vocaal=klinker).
Een staafdiagram helpt ons om in één oogopslag de belangrijkste kenmerken te bepalen van de verdeling van een discrete variabele: de meest kenmerkende (meest voorkomende) waarde, en de spreiding over categorieën. Voor de klankfrequenties in het Nederlands (Figuur 8.1) zien we dat bij de medeklinkers de plosieven het meeste voorkomen, dat bij de klinkers de korte klinkers het meeste voorkomen, dat tweeklanken weinig gebruikt worden (zgn. diphthongs, de klinkers in ei, ui, au), en dat er meer medeklinkers dan klinkers gesproken worden.
Tip: Vermijd schaduwen en andere 3D-effecten in een staafdiagram! De breedte en hoogte van een rechthoek wordt daardoor minder goed leesbaar, en de zichtbare oppervlakte van een beschaduwde rechthoek of van een balk correspondeert niet meer goed met de frequentie.
8.4 Histogrammen
Een histogram is de grafische weergave van een frequentieverdeling van een continue, numerieke variabele (van interval- of ratio-meetniveau). Een histogram is opgebouwd uit rechthoeken. De breedte van elke rechthoek correspondeert met de intervalbreedte (een rechthoek kan ook 1 eenheid breed zijn) en de hoogte correspondeert met de frequentie van dat interval of van die waarde. De oppervlakte van iedere rechthoek correspondeert dus met de frequentie. In tegenstelling tot een staafdiagram sluiten de rechthoeken op elkaar aan langs de horizontale as.
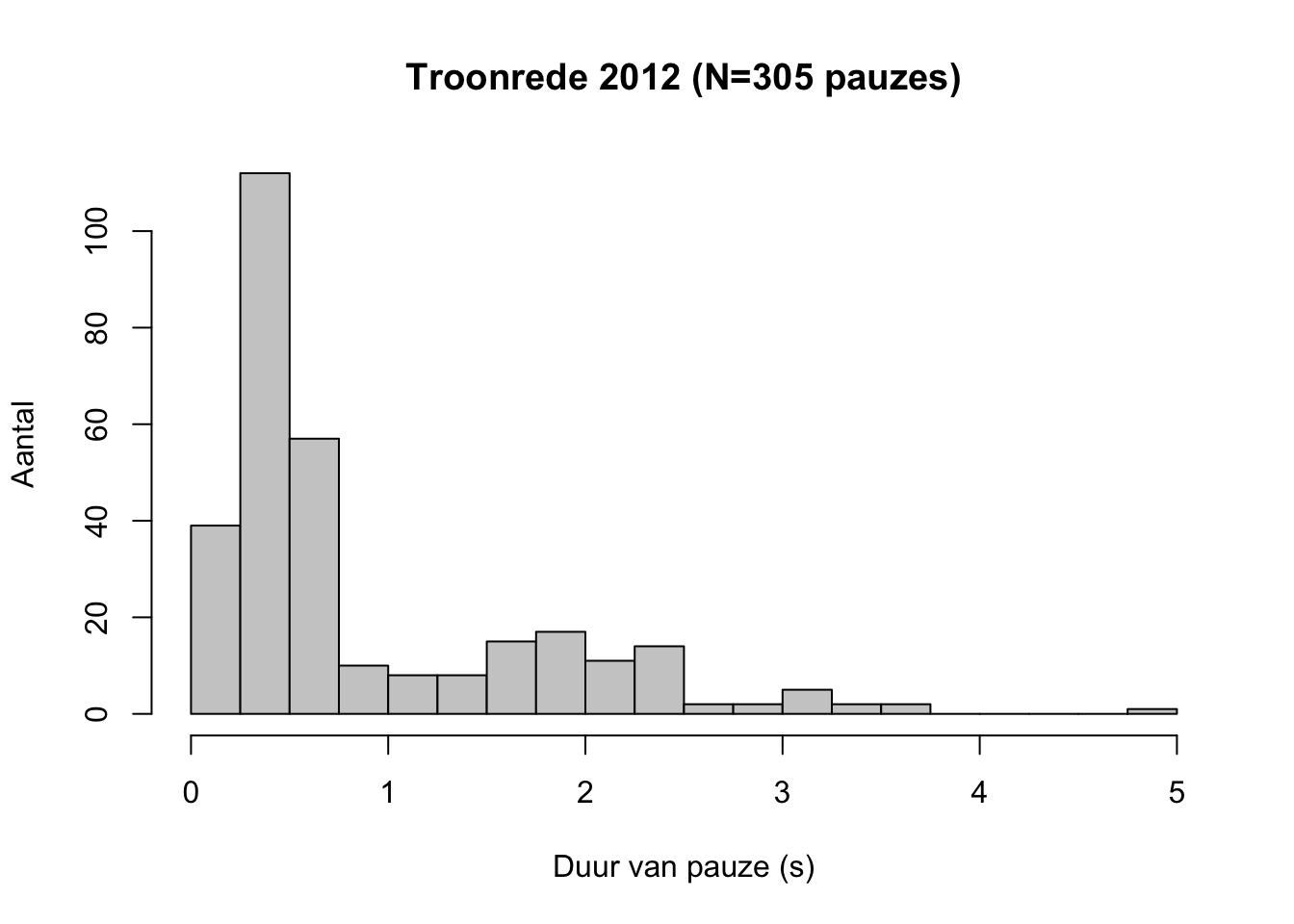
Figuur 8.2: Histogram van de duren van spreekpauzes (in seconden) in de Troonrede van 18 september 2012, voorgelezen door Koningin Beatrix (N=305).
Een histogram helpt ons om in één oogopslag de belangrijkste kenmerken te bepalen van de verdeling van een continue variabele: de meest kenmerkende (meest voorkomende) waarde, de mate van spreiding, het aantal pieken in de frequentieverdeling, de ligging van die pieken, en eventuele uitbijters (zie §9.4.2). Voor de pauzes in de Troonrede van 2012 (Figuur 8.2) zien we dat de meeste pauzes tussen 0.25 en 0.75 s duren (vermoedelijk zijn dat adempauzes), dat er twee pieken zijn in de verdeling (de tweede piek ligt bij 2 s), en dat er één extreem lange pauze is (met een duur van bijna 5 s).
Tip: Vermijd schaduwen en andere 3D-effecten in een histogram! De breedte en hoogte van een rechthoek wordt daardoor minder goed leesbaar, en de zichtbare oppervlakte van een beschaduwde rechthoek of van een balk correspondeert niet meer goed met de frequentie.
8.4.1 SPSS
Analyze > Descriptive Statistics > Frequencies...Selecteer variabele (sleep naar paneel “Variable(s)”).
Kies Charts, kies daarna Chart type: Bar chart voor een
staafdiagram of Chart type: Histogram voor een histogram (zie
bovenstaande tekst voor het verschil tussen deze opties).
Bevestig met OK.
8.4.2 JASP
Klik in de bovenbalk op Descriptives. Selecteer vervolgens de gewenste variabele(n) en plaats ze in het veld “Variables”. Klik de balk Plots open en vink Distribution plots aan onder “Basic plots”. Je zult zien dat JASP automatisch een staafdiagram maakt voor variabelen die het meetniveau “Ordinal” of “Nominal” hebben, en een histogram voor variabelen met meetniveau “Scale”. Zorg dus dat het meetniveau van alle variabelen goed staat ingesteld. Je kunt het meetniveau veranderen door in het data tabblad op het meetniveau-icoontje voor de variabele-naam te klikken.
8.4.3 R
Een staafdiagram zoals Figuur 8.1 maak je in R met de volgende commando’s:
# lees data
klankfreq <- read.table( file="data/klankfreq.txt", header=T )
# maak barplot van kolom `aantal` in dataset `klankfreq`
with( klankfreq, barplot( aantal, beside=T,
ylab="Aantal",
main="Klankfrequenties in het Nederlands (N=2968220)",
col=ifelse(klankfreq[,1]=="V","grey40","grey20") ) ) -> klankfreq_barplot
# maak labels langs onderste horizontale as
axis(side=1, at=klankfreq_barplot, labels=klankfreq$hoofdklasse)
axis(side=1, at=klankfreq_barplot, tick=F, line=1, labels=klankfreq$onderklasse )
# of eenvoudiger: with(klankfreq, barplot(aantal) ) # alle defaults Een histogram zoals in Figuur 8.2 maak je in R met de volgende commando’s:
# lees dataset
load(file="data/pauses6.Rda")
# haal daaruit pauzeduren (kolom 12) voor jaar 2012, in aparte variabele `troon2012`
troon2012 <- pauses6[ pauses6$jaar==2012, 12 ] # save col_12 as single vector
# maak histogram
hist( troon2012,
breaks=seq(0, 5, by=0.25),
col="grey80",
xlab="Duur van pauze (s)", ylab="Aantal",
main="Troonrede 2012 (N=305 pauzes)" ) -> troonrede2012pauzes_hist