Hoofdstuk 11 Samenhang

11.1 Inleiding

Het meeste empirische onderzoek is gericht op het vaststellen van samenhang tussen variabelen. In experimenteel onderzoek gaat het dan primair om de samenhang tussen onafhankelijke en afhankelijke variabelen. In het volgende deel gaan we nader in op diverse manieren om vast te stellen of er een “significant” (beduidend, betekenisvol, niet toevallig) verband bestaat tussen de onafhankelijke en afhankelijke variabele. Daarnaast kan de onderzoeker geïnteresseerd zijn in de onderlinge samenhang tussen meerdere afhankelijke variabelen, bijvoorbeeld de samenhang tussen de oordelen van meerdere beoordelaars (zie ook Hoofdstuk 12).

In quasi-experimenteel onderzoek is het onderscheid tussen onafhankelijke en afhankelijke variabelen doorgaans minder duidelijk. Er worden meerdere variabelen geobserveerd, en de onderzoeker is vooral geïnteresseerd in de onderlinge samenhang tussen die geobserveerde variabelen. Wat is bijvoorbeeld de samenhang tussen de scores voor lezen, rekenen, en wereldoriëntatie in het CITO-onderzoek (zie Tabel 9.1)? In dit hoofdstuk gaan we nader in op de manieren om die samenhang of correlatie uit te drukken in een getal: een correlatie-coëfficient. Afhankelijk van de meetniveau’s van de variabelen zijn er verschillende correlatie-coëfficiënten, die we verder in dit hoofdstuk zullen behandelen.

Het is raadzaam om altijd eerst een grafische weergave te maken van de samenhang tussen de variabelen, in de vorm van een zgn. spreidingsdiagram (ook vaak aangeduid als scattergram of scatterplot), zoals in Figuur 11.1. Ieder punt in dit spreidingsdiagram correspondeert met een leerling (of algemener, met een eenheid van de steekproef). De positie van ieder punt (leerling) wordt bepaald door de geobserveerde waarden van twee variabelen (hier is \(X\) score bij leestoets, \(Y\) is score bij rekentoets). Zo’n spreidingsdiagram helpt om een eventueel verband te interpreteren, en om te inspecteren of de observaties wel voldoen aan de randvoorwaarden om een correlatie te berekenen uit die observaties. Kijk in ieder geval naar (a) de aanwezigheid van een eventueel verband, (b) de vorm van dat verband (lineair, exponentieel, …), (c) eventuele uitbijters (extreme observaties, zie §9.4.2), en (d) de verdeling van de twee variabelen, zie §9.7.

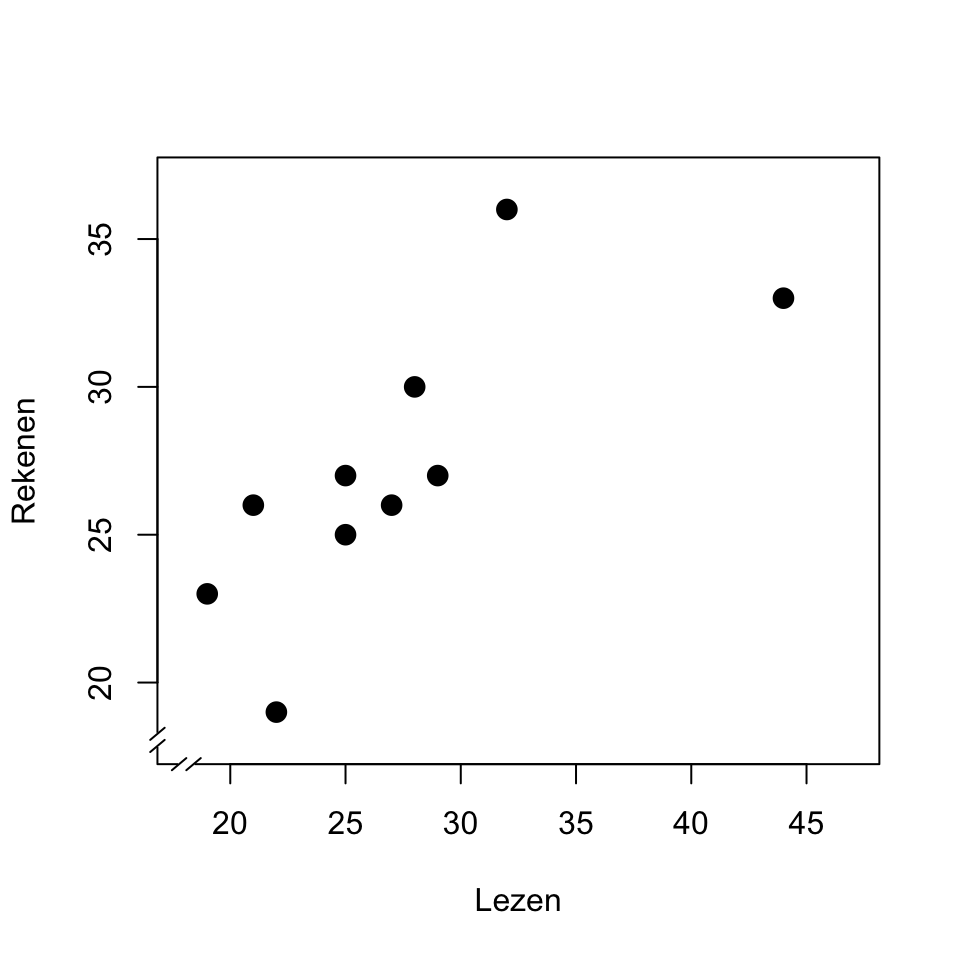
Figuur 11.1: Spreidingsdiagram van de scores van een leestoets en een rekentoets; zie tekst.

Dit spreidingsdiagram laat zien (a) dat er een verband bestaat tussen de scores bij lezen en bij rekenen. Het verband is (b) bij benadering lineair, d.w.z. te beschrijven als een rechte lijn; we komen daar op terug in §11.3. Het verband helpt ons ook om de spreiding in de twee variabelen te verklaren. Immers, de spreiding in de rekenscores is voor een deel te begrijpen of te verklaren uit de spreiding in de leestoets: leerlingen die een relatief goede score behalen bij lezen, doen dat ook bij rekenen. De observaties van de twee variabelen verschaffen dus niet alleen informatie over die twee variabelen zelf, maar bovendien over de samenhang tussen die variabelen. In dit spreidingsdiagram zien we overigens ook (c) dat de hoogste leesscore een uitbijter vormt (zie ook Fig.9.3); zulke uitbijters kunnen onevenredig grote invloed hebben op het gevonden verband.

11.2 Pearson product-moment-correlatie

De Pearson product-moment-correlatiecoëfficiënt wordt aangeduid met symbool \(r\) (in het geval van twee variabelen). Deze coëfficiënt is te gebruiken als beide variabelen geobserveerd zijn op het interval-meetniveau (§4.4), en als beide variabelen bij benadering normaal-verdeeld zijn (§10.3). De berekening doen we tegenwoordig per computer.

Voor de observaties in het spreidingsdiagram in Fig.11.1 vinden we een correlatie van \(r=+.79\). De correlatie-coëfficiënt is een getal dat per definitie ligt tussen \(-1\) en \(+1\). Een positieve correlatiecoëfficient wijst op een positief verband: een grotere waarde van \(X\) correspondeert met een grotere waarde van \(Y\). Een negatieve coëfficiënt wijst op een negatief verband: een grotere waarde van \(X\) correspondeert met een kleinere waarde van \(Y\). Een waarde van \(r\) dicht bij nul wijst op een zwak of afwezig verband: de spreiding in \(X\) heeft niets te maken met de spreiding in \(Y\); er is geen of alleen zwakke correlatie. Een correlatie van \(.4<r<.6\) (of \(-.6 < r < -.4\)) noemen we middelmatig. Een correlatie van \(r>.6\) (of \(r< -.6\)) wijst op een sterke samenhang. Als \(r=1\) (of \(r=-1\)) dan liggen alle observaties precies op een rechte lijn. Figuur 11.2 toont meerdere spreidingsdiagrammen met de bijbehorende correlatiecoëfficiënten.

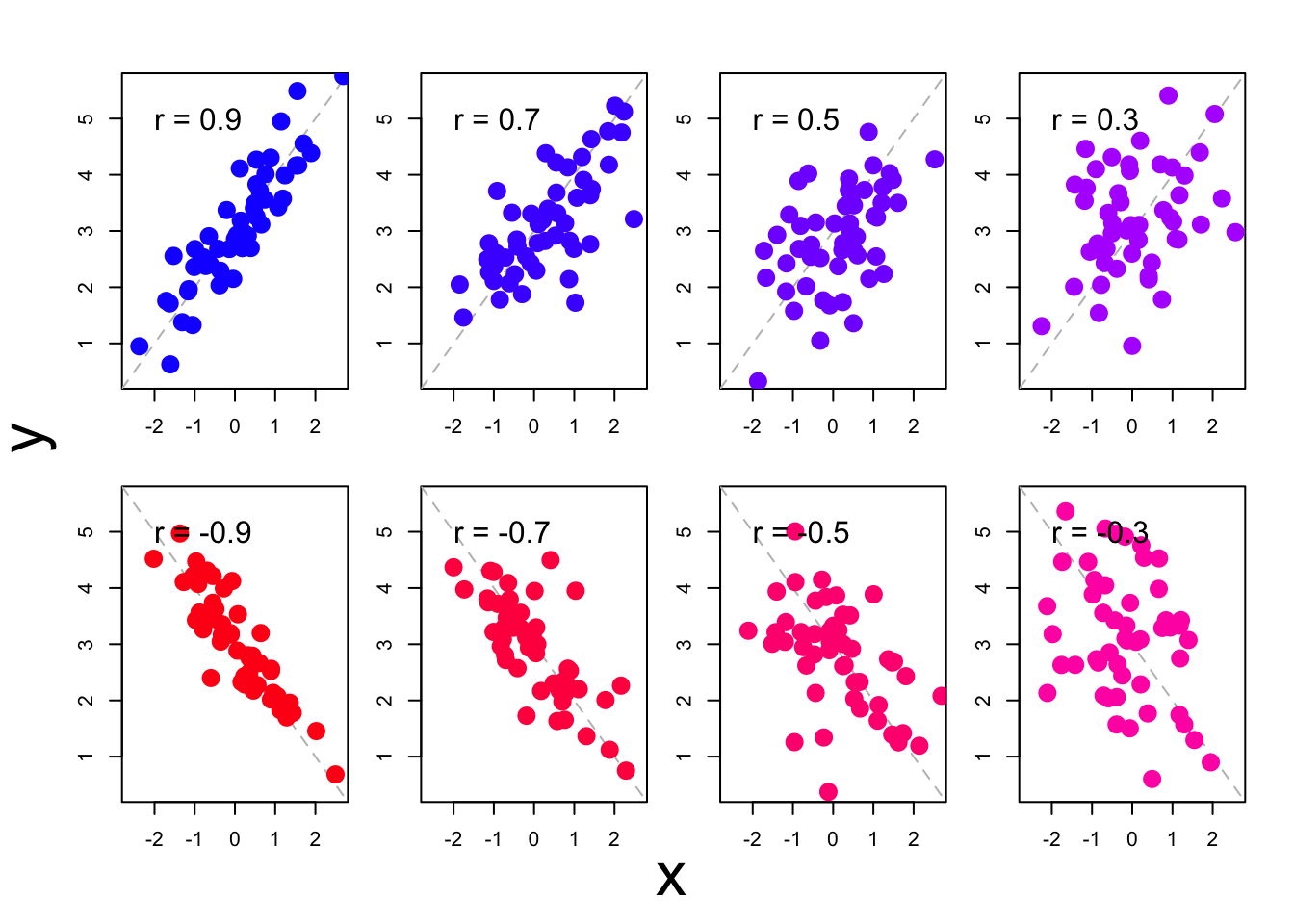
Figuur 11.2: Meerdere spreidingsdiagrammen van observaties met bijbehorende correlatiecoëfficiënten.

De correlatie die we zien tussen de scores van de twee variabelen (zoals \(r=.79\) tussen scores bij leestoets en rekentoets, Fig.11.1) zou ook het gevolg kunnen zijn van toevallige variaties in de observaties. Het is immers mogelijk dat de leerlingen met een goede score op de leestoets, zuiver door toeval, ook een goede score op de rekentoets hebben behaald — ook als er in de populatie eigenlijk niet samenhang is tussen de twee variabelen. De onbekende correlatie in de populatie duiden we aan met de griekse letter \(\rho\) (“rho”); het is dus ook mogelijk dat \(\rho=0\). Ook als \(\rho=0\) is het mogelijk om \(n=10\) leerlingen in de steekproef te hebben die hoge scores op het ene onderdeel toevallig combineren met hoge scores op het andere onderdeel (en om toevallig niet leerlingen in de steekproef te hebben die hoge scores op het ene onderdeel combineren met lage scores op het andere onderdeel). We kunnen schatten wat de kans \(p\) is om deze correlatie van \(r=0.79\) of sterker te vinden in een steekproef van \(n=10\) leerlingen, indien de samenhang in de populatie eigenlijk nihil is (d.i. indien \(\rho=0\)). Deze kans \(p\) noemen we de significantie van de correlatiecoëfficiënt; we komen in Hoofdstuk 13 uitgebreider terug op dit begrip ‘significantie’. Daarop vooruitlopend: als deze kans \(p\) kleiner is dan \(.05\), dan nemen we aan dat de gevonden correlatie \(r\) niet toevallig, d.i. significant is. Vaak zien we een kleine kans \(p\) bij een sterke correlatie \(r\). De correlatiecoëfficiënt \(r\) geeft de richting en sterkte van het verband aan, en de significantie \(p\) geeft de kans aan om dit verband bij toeval te vinden als \(\rho=0\) in de populatie. We rapporteren deze bevindingen als volgt²³:

---

Voorbeeld 11.1: De scores van de \(n=10\) leerlingen op de deeltoetsen van de CITO-toets in Tabel 9.1 laten een sterke correlatie zien tussen de scores bij de onderdelen Lezen en Rekenen: Pearson \(r=0.79, p=.007\). Leerlingen met een relatief hoge score bij het ene onderdeel behalen in het algemeen ook een relatief hoge score bij het andere onderdeel.

---

In veel onderzoeken zijn we geïnteresseerd in de correlaties tussen meer dan twee variabelen. Die correlaties tussen variabelen worden dan vaak gerapporteerd in een zgn. correlatiematrix zoals Tabel 11.1, dat is een tabel waar de correlaties vermeld worden van alle paren van correlaties (Eng. ‘pairwise correlation matrix’).

Tabel 11.1: Correlaties tussen de drie onderdelen van de CITO-toets, zoals samengevat in Tabel 9.1, met bijbehorende significantie-niveau tussen haakjes.

	Lezen	Rekenen	Wereldoriëntatie
Lezen	1.00
Rekenen	.79 (.007)	1.00
Wereldoriëntatie	-.51 (.13) -	.01 (.97)	1.00

In deze matrix is alleen de onderste (linker) helft van de volledige matrix weergegeven. Dat is ook voldoende, want de cellen zijn gespiegeld rond de diagonaal: de correlatie tussen Lezen (kolom 1) en Rekenen (rij 2) is immers hetzelfde als de correlatie tussen Rekenen (kolom 2) en Lezen (rij 1). De cellen op de diagonaal van de correlatiematrix bevatten altijd de waarde \(1.00\), omdat een variabele altijd perfect met zichzelf correleert. We rapporteren deze bevindingen als volgt:

---

Voorbeeld 11.2: De paarsgewijze correlaties tussen scores van de \(n=10\) leerlingen op de drie deeltoetsen van de CITO-toets zijn samengevat in Tabel 11.1. We zien een sterke correlatie tussen de scores bij de onderdelen Lezen en Rekenen: leerlingen met een relatief hoge score bij het onderdeel Lezen behalen in het algemeen ook een relatief hoge score bij het onderdeel Rekenen. De overige correlaties waren niet significant.

---

11.2.1 Formules

De eenvoudigste formule voor de Pearson product-moment-correlatiecoëfficiënt \(r\) maakt gebruik van de standaard-normaal-scores die we al eerder gebruikt hebben (§9.8): \[\begin{equation} r_{XY} = \frac{\sum z_X z_Y}{n-1} \tag{11.1} \end{equation}\]

Net als bij het berekenen van de variantie (formule (9.3)) delen we weer door \((n-1)\) om een schatting te maken van de samenhang in de populatie.

11.2.2 SPSS

Voor Pearson’s product-moment-correlatiecoëfficiënt:

Analyze > Correlate > Bivariate...

Kies Pearsons correlatiecoëfficiënt, vink aan: Flag significant correlations. Bevestig met OK. De resulterende uitvoer (tabel) voldoet niet aan de stijl-eisen; je moet de gegevens dus overnemen in of omzetten naar een eigen tabel die daar wel aan voldoet.

11.2.3 JASP

Voor Pearson’s product-moment-correlatiecoëfficiënt klik je in de bovenbalk op:

Regression > Classical: Correlation

Selecteer de variabelen waarvan je de correlatie wilt berekenen in het veld “Variables”. Zorg dat onder “Sample Correlation Coefficient” Pearson's r aangevinkt is, en onder “Additional Options” Report significance, Flag significant correlations en Sample size. Je kunt ook Display pairwise aanvinken voor een simpelere tabel als uitvoer. In beide gevallen is de uitvoer tabel niet volgens de stijl-eisen; neem de gegevens dus over om het netjes te rapporteren.

11.2.4 R

cito <- read.table(file="data/cito.txt", header=TRUE)
cor( cito[,2:4] ) # correlatie-matrix van kolommen 2,3,4

##                       Lezen    Rekenen Wereldoriëntatie
## Lezen             1.0000000 0.74921033      -0.50881738
## Rekenen           0.7492103 1.00000000       0.06351024
## Wereldoriëntatie -0.5088174 0.06351024       1.00000000

with( cito, cor.test( Lezen, Rekenen ) )

## 
##  Pearson's product-moment correlation
## 
## data:  Lezen and Rekenen
## t = 3.1994, df = 8, p-value = 0.01262
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.2263659 0.9368863
## sample estimates:
##       cor 
## 0.7492103

11.3 Regressie

Het meest eenvoudige verband dat we kunnen onderscheiden en beschrijven is een lineair verband, d.w.z. een rechte lijn in het spreidingsdiagram (zie Fig.11.2). Deze rechte lijn geeft aan welke waarde van \(Y_i\) voorspeld wordt, op basis van de waarde van \(X_i\). Deze voorspelde waarde van \(Y_i\) wordt genoteerd als \(\widehat{Y_i}\) (“Y-hat”). De beste voorspelling \(\widehat{Y_i}\) is gebaseerd op de waarde van \(X_i\) èn op het lineaire verband tussen \(X\) en \(Y\): \[\begin{equation} \widehat{Y_i} = a + b {X_i} \tag{11.2} \end{equation}\]
De rechte lijn wordt beschreven met twee parameters, nl. het begingetal \(a\) (Eng. ‘intercept’) en de hellingscoëfficiënt \(b\) (Eng. ‘slope’)²⁴. De rechte lijn die het lineaire verband beschrijft wordt ook aangeduid als de “regressielijn”; we proberen immers om de geobserveerde waarden van \(Y\) te herleiden tot deze lineaire functie van de waarden van \(X\).

Het verschil tussen de geobserveerde waarde \(Y\) en de voorspelde waarde \(\widehat{Y}\) \((Y-\widehat{Y})\) wordt het residu genoemd (symbool \(e\)). Anders gezegd, de geobserveerde waarde wordt beschouwd als de optelsom van twee componenten, nl. de voorspelde waarde en het residu: \[\begin{align} Y &= \widehat{Y} + e \\ &= a + b X + e \tag{11.3} \end{align}\]

Bovenstaande gedachtengang wordt geïllusteerd in het spreidingsdiagram in Figuur 11.3. De stippellijn geeft het lineaire verband aan tussen de twee toetsen: \[\begin{equation} \widehat{\textrm{Rekenen}} = 12.97 + 0.52 \times \textrm{Lezen} \tag{11.4} \end{equation}\]

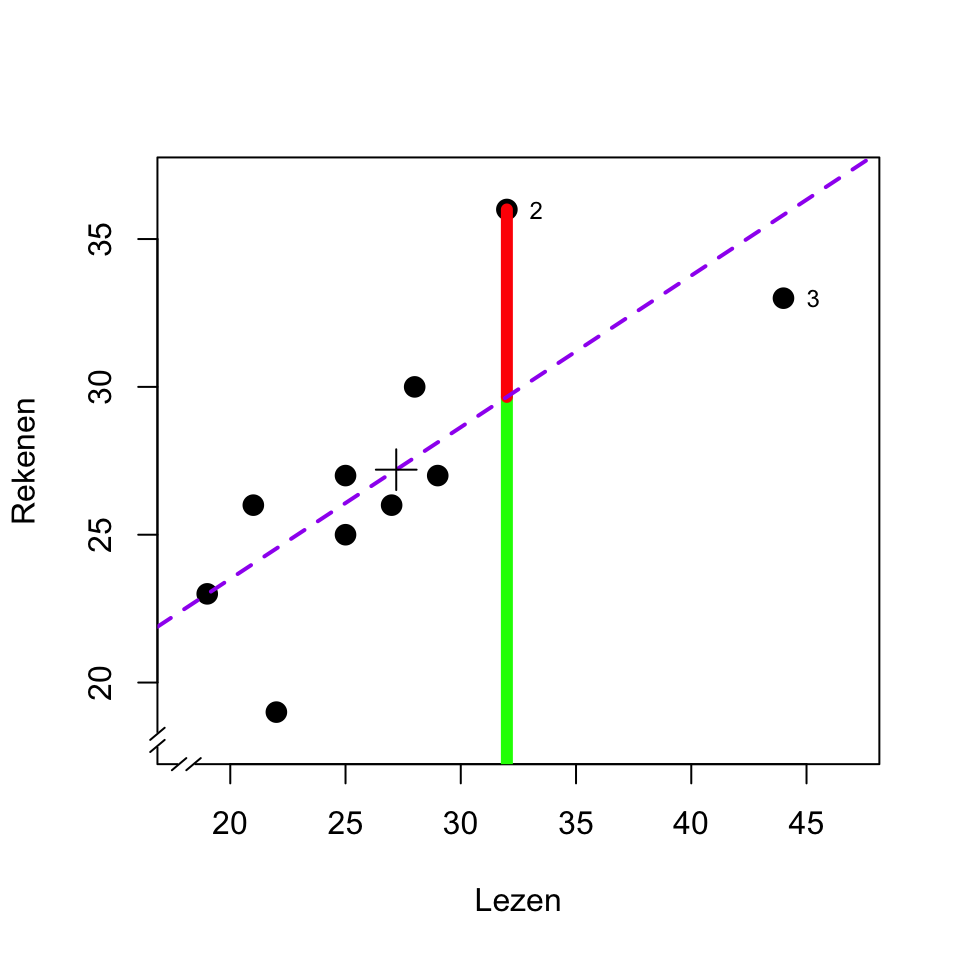
Figuur 11.3: Spreidingsdiagram van de scores van een leestoets en een rekentoets. In het diagram is tevens aangegeven de regressielijn (stippellijn), de voorspelde waarde (groen) en residu (rood) van de rekentoets voor leerling 2, de gemiddelden (plus-symbool), en markeringen voor leerling 2 en 3; zie tekst.

Deze stippellijn geeft dus aan wat de voorspelde waarde \(\widehat{Y}\) is voor iedere waarde van \(X\). Voor de tweede leerling met \(X_2 = 32\) voorspellen we zo \(\widehat{Y_2} = 12.97 + (0.52) (32) = 29.61\) (voorspelde waarde, groene lijnstuk). Voor alle observaties die niet precies op deze regressielijn liggen (stippellijn), is er een afwijking tussen de voorspelde score \(\widehat{Y}\) en de geobserveerde score \(Y\) (residu, rode lijnstuk). Voor de tweede leerling is deze afwijking \(e_2 = (Y_2 - \widehat{Y_2}) = (36-29.61) = 6.49\) (residu, rode lijnstuk).

Zoals gezegd worden de geobserveerde waarden van \(Y\) beschouwd als de optelsom van twee componenten, de voorspelde waarde \(\widehat{Y}\) (groen) en het residu \(e\) (rood). Op dezelfde wijze kan ook de totale variantie van \(Y\) beschouwd worden als de optelsom van de twee varianties van deze componenten: \[\begin{equation} s^2_{Y} = s^2_{\widehat{Y}} + s^2_e \tag{11.5} \end{equation}\] Van de totale variantie \(s^2_Y\) van Y is dus het ene deel (\(s^2_{\widehat{Y}}\)) te herleiden tot c.q. te verklaren uit de variantie van \(X\), via het lineaire verband beschreven met parameters \(a\) en \(b\) (zie formule (11.2)), en het andere deel (\(s^2_e\)) is niet te herleiden of te verklaren. Dat tweede deel, de niet-voorspelde variantie van de residuen, wordt ook wel de ‘residuele variantie’ of ‘ruis’ genoemd.

Als we \(Y\) goed kunnen voorspellen uit \(X\), d.w.z. als de Pearson product-moment-correlatiecoëfficiënt \(r\) hoog is (Fig. 11.2, links), dan zijn de residuen \(e\) dus relatief klein, de observaties liggen dicht rond de regressielijn in het spreidingsdiagram, en dan is dus ook de residuele variantie \(s^2_e\) relatief gering. Omgekeerd, als we \(Y\) niet goed kunnen voorspellen uit \(X\), d.w.z. als de correlatiecoëfficiënt \(r\) relatief laag is (Fig. 11.2, rechts), dan zijn de residuen \(e\) dus relatief groot, de observaties liggen wijd verspreid rond de regressielijn in het spreidingsdiagram, en dan is dus ook de residuele variantie \(s^2_e\) relatief groot. Het kwadraat van de Pearson product-moment-correlatiecoëfficiënt \(r\) geeft aan wat de relatieve omvang is van de twee variantie-componenten, ten opzichte van de totale variantie: \[\begin{align} r^2 & = \frac{s^2_{\widehat{Y}}}{s^2_Y} \\ & = 1 - \frac{s^2_e}{s^2_Y} \tag{11.6} \end{align}\] Deze grootheid \(r^2\) wordt ook wel aangeduid als de “proportie verklaarde variantie” of als de “determinatie-coëfficiënt”.

De waarden van de lineaire parameters \(a\) en \(b\) in formule (11.2) worden zo gekozen dat de verzamelde residuen zo klein mogelijk zijn, d.w.z. dat de residuele variantie \(s^2_e\) zo klein mogelijk is (“least squares fit”), en dus \(r^2\) zo groot mogelijk (zie §11.3.1). Op die manier vinden we een rechte lijn die het beste past bij de observaties van \(X\) en \(Y\).

Een lineaire regressie kan worden gerapporteerd als volgt:

---

Voorbeeld 11.3: Uit een lineaire-regressie-analyse blijkt dat de score bij Rekenen samenhangt met die bij Lezen: \(b=0.51, r=.79, p_r=.007\), over \(n=10\) leerlingen. Dit lineaire regressiemodel verklaart \(r^2=.51\) van de totale variantie in de rekenscores (de residuele standaarddeviatie is \(s_e= \sqrt{82.803/(n-1-1)} = 3.22\)).

---

11.3.1 Formules

Bij lineaire regressie van \(y\) op \(x\) proberen we de coëfficiënten \(a\) en \(b\) zodanig te schatten dat (het kwadraat van) de afwijking tussen de voorspelde waarde \(\hat{y}\) en de geobserveerde waarde \(y\) zo klein mogelijk is, m.a.w. dat het kwadraat van de residuen \((y-\hat{y})\) zo klein mogelijk is. Dit wordt de “least squares” methode genoemd (zie http://www.itl.nist.gov/div898/handbook/pmd/section4/pmd431.htm).

De beste schatting voor \(b\) is \[b = \frac{ \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y}) } { \sum_{i=1}^n (x_i-\overline{x})^2 }\]

De beste schatting voor \(a\) is \[a = \overline{y} - b \overline{x}\]

11.3.2 SPSS

Voor lineaire regressie:

Analyze > Regression > Linear...

Kies Dependent variable: Rekenen en kies Independent variable: Lezen. Onder de knop Statistics, vink aan Model fit, vink aan R squared change, kies Estimates, en daarna Continue.
Onder de knop Plot, vink aan Histogram en vink ook aan Normal probability plot; deze keuzes zijn vereist om een numerieke(!) samenvatting te krijgen over de residuals.
Onder de knop Options, kies Include constant om ook de constante coëfficiënt \(a\) te laten berekenen. Bevestig alle keuzes met OK.

De resulterende uitvoer omvat meerdere tabellen en figuren; deze kan je niet rechtstreeks overnemen in je verslag. De tabel getiteld Model Summary bevat de correlatie-coëfficiënt, hier aangeduid met hoofdletter \(R=.749\).
De tabel getiteld Coefficients bevat de regressie-coëfficienten. De regel met aanduiding (Constant) vermeldt coëfficient \(a=13.25\); de regel getiteld Lezen vermeldt coëfficient \(b=0.51\).
De tabel getiteld Residual Statistics geeft informatie over zowel de voorspelde waarden als de residuen. Controleer of het gemiddelde van de residuen inderdaad nul is. In deze tabel zien we ook (regel 2, kolom 4) dat de standaarddeviatie van de residuen \(3.212\) is.

11.3.3 JASP

Voor lineaire regressie klik je in de bovenbalk op:

Regression > Classical: Linear Regression

Selecteer de variabele Rekenen in het veld “Dependent Variable”, en de variabele Lezen in het veld “Covariates”. Klik vervolgens de balk Model open en controleer of Lezen onder “Model Terms” staat. Ook moet Include intercept aangevinkt zijn, om de constante coëfficiënt \(a\) te laten berekenen. Open ook de balk Statistics en zorg dat Estimates, Model fit en R squared change aangevinkt zijn. Vink onder “Residuals” ook Statistics aan om een numerieke samenvatting te krijgen over de residuals. Onder de balk Plots mogen ook Residuals vs. histogram en Q-Q plot standardized residuals worden aangevinkt voor een weergave van de residuals.

De resulterende uitvoer omvat meerdere tabellen en figuren; deze kan je niet rechtstreeks overnemen in je verslag. De tabel getiteld Model Summary bevat de correlatie-coëfficiënt, hier aangeduid met hoofdletter \(R=.749\).
De tabel getiteld Coefficients bevat de regressie-coëfficienten. De regel met aanduiding (Intercept) vermeldt coëfficient \(a=13.25\); de regel getiteld Lezen vermeldt coëfficient \(b=0.51\).
De tabel getiteld Residual Statistics geeft informatie over zowel de voorspelde waarden als de residuen. Controleer of het gemiddelde van de residuen inderdaad (zo goed als gelijk aan) nul is. In deze tabel zien we ook (regel 2, kolom 4) dat de standaarddeviatie van de residuen \(3.212\) is.

11.3.4 R

summary( m1 <- lm( Rekenen~Lezen, data=cito ) )

## 
## Call:
## lm(formula = Rekenen ~ Lezen, data = cito)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.5332 -1.1167 -0.5332  1.7168  6.3384 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)  
## (Intercept)  13.2507     4.4910   2.950   0.0184 *
## Lezen         0.5128     0.1603   3.199   0.0126 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.406 on 8 degrees of freedom
## Multiple R-squared:  0.5613, Adjusted R-squared:  0.5065 
## F-statistic: 10.24 on 1 and 8 DF,  p-value: 0.01262

Het command lm specificeert een lineair regressiemodel, met Rekenen als afhankelijke variabele en Lezen als predictor. Dit model wordt bewaard als een object genaamd m1, en dat wordt meteen weer gebruikt als argument (invoer) om te rapporteren. In die rapportage van model m1 wordt de constante coëfficient \(a\) aangeduid als Intercept.

sd( resid( m1 ) ) # s.d. van residuen volgens `m1`

## [1] 3.211533

11.4 Invloedrijke observaties

In de vorige paragraaf zagen we dat in een correlatie-analyse of een regressie-analyse gestreefd wordt naar een minimale residuele variantie. Eerder zagen we al ook dat uitbijters of extreme observaties, per definitie, relatief veel bijdragen aan de variantie. Bij elkaar leidt dat ertoe, dat uitbijters of extreme observatie grote invloed kunnen hebben op de hoogte van de correlatie, of op de gevonden regressie (het gevonden lineaire verband). Dat is ook te zien in Fig.11.3. Leerling 3 heeft een extreem hoge score bij Lezen (zie ook Fig.9.3). Als we deze leerling 3 buiten beschouwing laten dan zou er niet veel veranderen aan de correlatie (\(r_{-3}=.79\)) maar wel aan de helling van de regressielijn (\(b=0.84\), ruim anderhalf keer zo groot als mèt leerling 3). Deze observatie “trekt” dus hard aan de regressielijn, juist omdat deze observatie een extreme waarde heeft voor \(X\) en daardoor veel invloed heeft.

Ook niet-extreme observaties kunnen toch van grote invloed zijn op de correlatie en regressie, als ze ver verwijderd zijn van de regressielijn en dus een grote bijdrage leveren aan de residuele variantie. Ook dat is te zien in Fig.11.3. Leerling 2 heeft geen extreme scores, maar heeft wel het grootste residu. Als we deze leerling 2 buiten beschouwing laten dan zou de correlatie aanzienlijk hoger zijn (\(r_{-2}=.86\)) maar de helling van de regressielijn zou slechts weinig veranderen (\(b=0.45\)).

Bij een correlatie-analyse of regressie-analyse moet je daarom altijd een spreidingsdiagram maken en bestuderen, om te kijken in hoeverre de resultaten beïnvloed zijn door een of enkele observaties. Let daarbij speciaal op observaties die ver verwijderd zijn van het gemiddelde, voor elk van beide variabelen, en op observaties die ver verwijderd zijn van de regressielijn.

11.5 Spearmans rangorde-correlatie

De beide variabelen waarvan we de correlatie willen onderzoeken, zijn niet altijd uitgedrukt op het interval-meetniveau (§4.4), of de onderzoekers willen of kunnen niet aannemen dat de beide variabelen bij benadering normaal-verdeeld zijn (§10.3). In dat geval is de product-moment-correlatie minder geschikt om de samenhang te kwantificeren. Indien de gegevens wel op ordinaal meetniveau zijn uitgedrukt, dan kunnen we wel andere correlatiecoëfficiënten gebruiken om de samenhang uit te drukken: Spearmans rangorde-correlatiecoëfficiënt (\(r_s\)) en Kendalls \(\tau\) (de griekse letter “tau”). Deze beide coëfficiënten zijn gebaseerd op de rangordening van de observaties; deze correlaties kunnen we dus altijd uitrekenen als we de observaties kunnen ordenen. Ook deze berekening doen we tegenwoordig per computer. In dit hoofdstuk bespreken we alleen de Spearmans rangorde-correlatiecoëfficiënt.

De Spearman rangorde-correlatiecoëfficiënt is gelijk aan de Pearson product-moment-correlatiecoëfficiënt toegepast op de rangnummers van de observaties. We zetten iedere observatie van een variabele om naar het volgorde-nummer, van de kleinste geobserveerde waarde (volgnummer 1) naar de grootste geobserveerde waarde (volgnummer \(n\)). Als twee of meer observaties dezelfde waarde hebben, dan krijgen ze ook hetzelfde (gemiddelde) rangnummer. In Tabel 11.2 zie je de rangnummers van de scores voor Lezen en Rekenen, hier geordend volgens de rangnummers voor Lezen.

Tabel 11.2: Rangnummers van de scores van 10 leerlingen op onderdelen van een toets, zoals samengevat in Tabel 9.1, met verschil \(v_i\) tussen de twee rangnummers per leerling.

Leerling	1	9	6	4	10	8	5	7	2	3
Lezen	1	2	3	4.5	4.5	6	7	8	9	10
Rekenen	2	4	1	4	6.5	4	8	6.5	10	9
verschil \(v_i\)	-1	-2	1	0.5	-2	2	-1	1.5	-1	1

De ordening in Tabel 11.2 maakt in één oogopslag duidelijk dat de drie leerlingen met de laagste score voor Lezen (nrs. 1, 9, 6) ook bijna de laagste scores voor Rekenen behaalden. Dat wijst op een positief verband. De twee beste lezers (nrs. 2 en 3) zijn ook de twee beste rekenaars. Ook dat wijst op een positief verband. Er is echter geen sprake van een perfect positief verband (dus hier \(r_s<1\)), want dan zouden de beide rangordeningen perfect overeen komen.

Bedenk zelf hoe Tabel 11.2 er uit zou zien, als er een perfect negatief verband zou zijn (\(r_s=-1\)) tussen de scores bij Lezen en Rekenen, en hoe de tabel er uit zou zien als er geen enkel verband zou zijn (\(r_s=0\)) tussen deze scores.

11.5.1 Formules

De samenhang tussen de rangnummers van twee variabelen wordt uitgedrukt in de Spearman rangorde-correlatiecoëfficiënt: \[\begin{equation} r_s = 1 - \frac{6 \sum v_i^2}{n(n^2-1)} \tag{11.7} \end{equation}\] waarin \(v_i\) staat voor het verschil in rangnummers op beide variabelen voor respondent \(i\). De breuk in deze formule wordt groter, en \(r_s\) wordt dus kleiner, naarmate de verschillen tussen de rangnummers groter zijn. Deze formule is echter alleen bruikbaar als er geen “ties” (gedeelde rangnummers) zijn in de variabelen; voor de gegevens in Tabel 11.2 met “ties” in beide variabelen moeten we een andere formule gebruiken.

Zoals blijkt is de Spearmans rangorde-correlatie \(r_s\) niet gelijk aan de Pearson product-momentcorrelatie \(r\) bij deze geobserveerde scores. Indien voldaan wordt aan de voorwaarden voor de Pearson coëfficient, dan geeft deze Pearson product-moment-correlatiecoëfficiënt een betere schatting van de samenhang dan de Spearman rangorde-correlatiecoëfficiënt. Maar als er niet aan die voorwaarden voldaan wordt, dan is de Spearman coëfficiënt weer te prefereren. De Spearman coëfficiënt is onder andere minder gevoelig voor invloedrijke extreme observaties — dergelijke uitschieters leggen immers minder gewicht in de schaal, nadat we de ruwe scores vervangen hebben door de rangnummers.

11.5.2 SPSS

Voor Spearmans rangorde-correlatiecoëfficiënt:

Analyze > Correlate > Bivariate...

Kies Spearman rangorde-correlatiecoëfficiënt, vink aan: Flag significant correlations. Bevestig met OK. De resulterende uitvoer (tabel) voldoet niet aan de stijl-eisen; je moet de gegevens dus overnemen in of omzetten naar een eigen tabel die daar wel aan voldoet, en rapporteren volgens de gebruikelijke conventies voor correlatie-analyse.

11.5.3 JASP

Voor Spearmans rangorde-correlatiecoëfficiënt klik je in de bovenbalk op:

Regression > Classical: Correlation

Selecteer de variabelen waarvan je de correlatie wilt berekenen in het veld “Variables”. Zorg dat onder “Sample Correlation Coefficient” Spearman's rho aangevinkt is, en onder “Additional Options” Report significance, Flag significant correlations en Sample size. Je kunt ook Display pairwise aanvinken voor een simpelere tabel als uitvoer. In beide gevallen is de uitvoer tabel niet volgens de stijl-eisen; neem de gegevens dus over om het netjes te rapporteren.

11.5.4 R

with(cito, cor.test( Lezen,Rekenen, method="spearman" ) )

## Warning in cor.test.default(Lezen, Rekenen, method = "spearman"): Cannot
## compute exact p-value with ties

## 
##  Spearman's rank correlation rho
## 
## data:  Lezen and Rekenen
## S = 25.229, p-value = 0.00198
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.8470988

11.6 Phi

De beide variabelen waarvan we de samenhang willen onderzoeken, zijn zelfs niet altijd uitgedrukt op het ordinale meetniveau (Hoofdstuk 4). Zelfs als beide variabelen alleen op nominaal niveau gemeten zijn, dan kan er nog een correlatie berekend worden, nl. de phi-correlatiecoëfficiënt (symbool \(r_\Phi\), met griekse letter “Phi”). Deze correlatiecoëfficiënt is ook bruikbaar als één van de twee variabelen op nominaal niveau gemeten is, en de andere op ordinaal niveau.

Laten we bij ons voorbeeld met de CITO-toets aannemen dat de eerste vijf leerlingen uit een grote stad komen, en de laatste vijf van het platteland. De herkomst van de leerling vormt een nominale variabele, met 2 categorieën, hier willekeurig aangeduid als 1 resp. 0 (zie §4.2; een nominale variabele met precies 2 categorieën wordt ook een binomiale of dichotome variabele genoemd). We vragen ons nu af of er enige samenhang is tussen de herkomst van een leerling en de score bij het onderdeel Rekenen van de CITO-toets. De tweede variabele is van interval-niveau. We zetten deze om naar een nominaal meetniveau. Dat kan op vele manieren, en het is aan de onderzoeker om daarbij een verstandige keuze te maken. Wij kiezen hier voor de vaak gebruikte ‘mean split’: de ene categorie (laag, code 0) bestaat uit scores kleiner dan of gelijk aan het gemiddelde (§9.3.1), en de andere categorie uit scores groter dan het gemiddelde (hoog, code 1). De aantallen leerlingen in elk van de \(2\times 2\) categorieën vatten we samen in een kruistabel (Tabel 11.3).

Tabel 11.3: Kruistabel van \(n=10\) leerlingen, onderverdeeld naar herkomst (stad=1, platteland=0) en naar categorie van score bij het onderdeel Rekenen van een CITO-toets (‘mean split’, laag=0, hoog=1), met letter-aanduiding voor de aantallen observaties; zie tekst.

herkomst	laag (0)	hoog (1)	totaal
platteland (0)	5 (A)	0 (B)	5 (A+B)
stad (1)	2 (C)	3 (D)	5 (C+D)
totaal	7 (A+C)	3 (B+D)	10 (A+B+C+D)

De nominale correlatiecoëfficiënt \(r_\Phi\) is gelijk aan de Pearson product-moment-correlatiecoëfficiënt als we die zouden toepassen op de binomiale codes (0 en 1) van de observaties. Alle 5 de leerlingen van het platteland hebben een score bij Rekenen gelijk aan of lager dan gemiddeld (\(\overline{y}=\) 27.2); van de leerlingen uit de stad hebben er 2 een score (gelijk aan of) lager dan gemiddeld. Er is dus samenhang tussen de binomiale codes van de rijen (herkomst) en die van de kolommen (score-categorieën) in Tabel 11.3. Die samenhang wordt gekwantificeerd in de correlatiecoëfficiënt \(r_\Phi=0.65\) voor deze gegevens.

11.6.1 Formules

De nominale correlatiecoëfficiënt \(r_\Phi\) wordt berekend als volgt, waarbij de letters verwijzen naar de aantallen in de cellen van een kruistabel (zie Tabel 11.3): \[\begin{equation} r_\Phi = \frac{(AD-BC)}{\sqrt{(A+B)(C+D)(A+C)(B+D)}} \tag{11.8} \end{equation}\]

Voor het hierboven besproken voorbeeld vinden we dan \[ r_\Phi = \frac{(15-0)}{\sqrt{(5)(5)(7)(3)}} = \frac{15}{22.91} = 0.65 \]

11.6.2 SPSS

De dataset cito bevat al een variabele StadPlat die de herkomst van de leerlingen aangeeft. Maar volledigheidshalve leggen we toch uit hoe je zo’n variabele zelf kunt construeren.

11.6.2.1 nieuwe variabele construeren

Transform > Recode into different variables...

Kies Leerling als oude variabele en vul als nieuwe naam StadPlat2 in voor de nieuwe variabele. Geef aan dat de oude waarden in Range van 1 t/m 5 (oud) omgezet moeten worden naar de nieuwe waarde 1, en evenzo dat leerlingen 6 t/m 10 de nieuwe waarde 0 moeten krijgen voor de nieuwe variabele StadPlat.

Voor Rekenen is het wat ingewikkelder. Je moet eerst je eerdere omzettingsregels verwijderen (die betrekking hadden op StadPlat). Maak dan op dezelfde wijze weer een nieuwe variabele, genaamd Rekenen2. Alle waarden vanaf de laagste waarde tot het gemiddelde (\(27.2\)) worden omgezet naar nieuwe waarde 0 voor die nieuwe variabele. Alle waarden vanaf het gemiddelde (\(27.2\)) tot de hoogste waarde worden omgezet naar nieuwe waarde 1.

11.6.2.2 correlatie-analyse

Na dit voorbereidend werk kunnen we eindelijk \(r_\Phi\) gaan berekenen.

Analyze > Descriptives > Crosstabs...

Selecteer de variabelen StadPlat2 (in “Rows” paneel) en Reken2 (in “Columns” paneel) voor kruistabel 11.3.
Kies Statistics… en vink optie Phi and Cramer’s Vaan!
Bevestig eerst met Continue en daarna nogmaals met OK.

11.6.3 JASP

De dataset cito bevat al een variabele StadPlat die de herkomst van de leerlingen aangeeft. Maar volledigheidshalve leggen we toch uit hoe je zo’n variabele zelf kunt construeren.

11.6.3.1 nieuwe variabele construeren

Maak eerst een nieuwe variabele aan door op de +-button te klikken rechts van de naam van de laatste kolom in de dataset. Er verschijnt een paneel “Create Computed Column”, waar je een naam voor de nieuwe variabele kunt invullen, bijvoorbeeld StadPlat2. Ook kun je kiezen uit R en een aanwijshandje. Dit zijn de twee opties in JASP om formules te definiëren waarmee de nieuwe (lege) variabele wordt gevuld; met R code of handmatig. Hieronder wordt voor allebei de opties uitgelegd hoe we hiermee de herkomst variabele maken. Als laatste kun je aanvinken welk meetniveau de variabele moet krijgen. Voor de herkomst variabele zet je dit op Nominal. Klik vervolgens op Create Column om de nieuwe variabele aan te maken. De nieuwe variabele (kolom) verschijnt als meest rechtse in de data en is nog leeg.

Als R is aangeklikt als optie om de nieuwe variabele te definiëren, verschijnt er boven de data een veld met “#Enter your R code here :)”. Hier kan R code worden gegeven die met behulp van R functies de nieuwe variabele definieert. Vul de R code in en klik onderaan op Compute column om de lege variabele te vullen met de gekozen waardes.
Voor de herkomst variabele kunnen we de volgende code gebruiken:

ifelse(Leerling <= 5, 1, 0) 

Dit betekent: als de score op de oude variabele (Leerling) kleiner dan of gelijk is aan (<=) 5, dan wordt de score een 1, en anders een 0. Dus: if Leerling <= 5, then 1, else 0. Let op dat dit alleen werkt in JASP als de gebruikte variabele (Leerling) op “Scale” meetniveau staat (want alleen dan kun je wiskundige operatoren zoals <= gebruiken). Als het meetniveau van de variabele niet op “Scale” staat pas je dit aan door in het data tabblad op het meetniveau-icoontje voor de variabele-naam te klikken, en “Scale” te selecteren.

Als het aanwijshandje is aangeklikt als optie om de nieuwe variabele te definiëren, verschijnt er boven de data een veld met links daarvan de variabelen, boven wiskundige symbolen, en rechts een aantal functies. Hier kan handmatig de functie worden geselecteerd die de nieuwe variabele definieert. Klik onderaan op Compute column om de lege variabele vervolgens te vullen met de gekozen waardes.
Voor de herkomst variabele scrol je rechts van het veld bij de functies naar beneden en klik op ifElse(y). De functie verschijnt in het veld en hier kunnen “test”, “then” en “else” worden vervangen door de gewenste gegevens. Klik op “test” en selecteer bovenaan \(\leq\). Sleep vervolgens de variabele ‘Leerling’ naar de puntjes aan de linkerkant van het teken, en vul rechts \(5\) in. Vul voor “then” en “else” \(1\) en \(0\) in. Je hebt dan: ifElse(Leerling $\leq$ 5,1,0), en deze formule werkt hetzelfde als de R code van hierboven. Let ook hier op dat dit alleen werkt in JASP als de gebruikte variabele (Leerling) op “Scale” meetniveau staat (want alleen dan kun je wiskundige operatoren zoals \(\leq\) gebruiken).

Voor Rekenen maak je eerst ook weer een nieuwe variabele aan door op de +-button te klikken rechts van de naam van de laatste kolom in de dataset. Geef de nieuwe variabele een naam (Reken2), kies R of het aanwijshandje, en geef de variabele het meetniveau Nominal. Klik vervolgens op Create Column om de nieuwe variabele aan te maken. De nieuwe variabele (kolom) verschijnt als meest rechtse in de data en is nog leeg.

Als R is aangeklikt als optie om de nieuwe variabele te definiëren, kan de volgende code worden gebruikt:

ifelse(Rekenen < mean(Rekenen), 0, 1)

Dit betekent: als de score op de oude variabele (Rekenen) kleiner is dan (<) de gemiddelde score (mean(Rekenen)), dan wordt de score een 0, en anders een 1. Dus: if Rekenen < mean(Rekenen), then 0, else 1. Vul de R code in en klik onderaan op Compute column om de lege variabele te vullen met de gekozen waardes.

Als het aanwijshandje is aangeklikt als optie om de nieuwe variabele te definiëren, selecteer je weer de functie ifElse(y). Klik op “test” en selecteer bovenaan \(<\). Sleep vervolgens de variabele ‘Rekenen’ naar de puntjes aan de linkerkant van het teken, en sleep de functie mean(y) (uit het scrolmenu rechts) naar de puntjes aan de rechterkant. Sleep de variabele ‘Rekenen’ nu ook naar de plek waar “values” staat. Vul voor “then” en “else” \(0\) en \(1\) in. Je hebt dan: ifElse(Rekenen < mean(Rekenen),0,1), en deze formule werkt hetzelfde als de R code van hierboven. Klik op Compute column om de lege variabele te vullen met de gekozen waardes.

11.6.3.2 correlatie-analyse

Na dit voorbereidend werk kunnen we eindelijk \(r_\Phi\) gaan berekenen. Klik in de bovenbalk op:

Frequencies > Classical: Contingency Tables

Selecteer de variabelen StadPlat2 (in het “Rows” paneel) en Reken2 (in het “Columns” paneel) voor kruistabel 11.3. Open de Statistics balk en vink Phi and Cramer’s Vaan onder “Nominal”. De waarde voor \(r_\Phi\) verschijnt dan ook in de uitvoer (als “Phi-coefficient”).

11.6.4 R

De dataset cito bevat al een variabele StadPlat die de herkomst van de leerlingen aangeeft. Maar volledigheidshalve laten we toch zien hoe je zo’n variabele zelf kunt construeren.

11.6.4.1 nieuwe variabele construeren

StadPlat2 <- ifelse( cito$Leerling<6, 1, 0) # 1=stad, 0=plat
Reken2 <- ifelse( cito$Rekenen>mean(cito$Rekenen), 1, 0 ) # 1=hoog, 0=laag

Maak een nieuwe variabele Reken2, met de waarde 1 indien de score voor Rekenen groter is dan het gemiddelde, en anders de waarde 0.

11.6.4.2 correlatie-analyse

Ook in R maken we eerst een kruistabel (Tabel 11.3) en daarna berekenen we de \(r_\Phi\) over die kruistabel.

print( table(StadPlat2,Reken2) -> citokruistabel ) # maak en bewaar en toon kruistabel

##          Reken2
## StadPlat2 0 1
##         0 5 0
##         1 2 3

if (require(psych)) { # voor psych::phi
  phi(citokruistabel) # eerder gemaakte kruistabel is hier invoer!
}

## Loading required package: psych

## [1] 0.65

11.7 Tenslotte

Bij het einde van dit hoofdstuk willen we nog eens benadrukken dat een samenhang of correlatie tussen twee variabelen niet noodzakelijkerwijs betekent dat er ook een causaal verband is tussen de variabelen, m.a.w. een samenhang betekent niet dat de ene variabele (bijv. behandeling) de oorzaak is en de andere variabele (bijv. genezing) het gevolg daarvan. De gangbare zegswijze daarvoor is “correlation does not imply causation,” zie ook Voorbeeld 6.1 (Hoofdstuk 6) en bijgaande Figuur 11.4 (met toestemming ontleend aan https://xkcd.com/552).

Figuur 11.4: Correlation does not imply causation.

---

23. Als de gevonden correlatie \(r\) niet significant is, dan kan die dus ook toevallig zijn, en dan laten we een interpretatie van de samenhang dus achterwege. We vermelden in ons verslag dan wel de gevonden correlatiecoëfficiënt en de gevonden significantie daarvan.↩︎

24. In schoolboeken wordt deze vergelijking ook wel beschreven als \(Y = a X + b\), met \(a\) als hellingscoëfficiënt en \(b\) als begingetal; we houden ons hier echter aan de internationaal gangbare notatie.↩︎