Hoofdstuk 13 Toetsing

13.1 Inleiding

Vanaf dit hoofdstuk houden we ons bezig met het toetsen van onderzoekshypothesen, en in het bijzonder met toetsen van nul-hypotheses (null hypothesis significance testing, NHST), zoals uitgelegd in Hoofdstuk 2.

Voor dergelijke toetsingen is in de loop der jaren een groot aantal technieken ontwikkeld. De toetsen die we behandelen zijn de meest gebruikte en kunnen we indelen in parametrische en non-parametrische toetsen. Parametrische toetsen veronderstellen dat de afhankelijke variabele (tenminste) gemeten is op intervalniveau (zie hoofdstuk 4), en dat de gemeten uitkomsten of scores normaal verdeeld zijn (zie §10.3 en §10.5). Bij non-parametrische toetsen worden, afhankelijk van de techniek, minder aannamen gemaakt over het meetniveau, danwel over de verdeling van de geobserveerde scores; het zijn zogenaamde verdelingsvrije toetsen. Het gevolg is dat de toetsing iets minder ‘gevoelig’ is, onder verder gelijke omstandigheden, d.w.z. dat de nulhypothese onder verder gelijke omstandigheden minder vaak verworpen kan worden. Deze toetsen hebben derhalve minder power (zie Hoofdstuk 14). Onderzoekers geven daarom meestal de voorkeur aan parametrische toetsen.

Het algemene principe van toetsing hebben we al kort besproken in §2.4 en §2.5. We leggen het hier nogmaals uit aan de hand van een voorbeeld. We onderzoeken de bewering H1: ‘studenten Taalwetenschap beheersen de traditionele zinsgrammatica beter dan de gemiddelde talen-student’. Als meet-instrument gebruiken we de zgn. “grammaticatoets”29 die verplicht is voor de meeste studenten in het talen-domein van de Universiteit Utrecht. Op grond van eerdere studiejaren verwachten we een gemiddelde score van 73 op deze toets; dit is het gemiddeld aantal goede antwoorden uit 100 vragen. We operationaliseren dus eerst H1: \(\mu > 73\), en daaruit leiden we de bijbehorende nulhypothese af die daadwerkelijk getoetst wordt: \(\mu = 73\). (In §13.4 hieronder gaan we nader in op het al dan niet noemen van de richting van het verschil in H1).

Voor de eerstejaars studenten Taalwetenschap (\(n=34\)) van een bepaald studiejaar vinden we een gemiddelde score van 84.4. Dat is inderdaad ver boven de referentie-waarde van 73, maar dat zou ook toeval kunnen zijn. Misschien is H0 waar, en zitten er geheel toevallig veel grammaticale bollebozen in onze steekproef (uit de populatie van mogelijke eerstejaars studenten Taalwetenschap). We kunnen de kans \(P\) op die situatie uitrekenen, d.w.z. de kans \(P\) om een gemiddelde score van \(\overline{x}=84.4\) te vinden gegeven een willekeurige steekproef van \(n=34\) personen en gegeven dat H0 in werkelijkheid waar is (d.w.z. \(\mu=73\)): dan blijkt \(P=.000000001913\). Deze kans \(P\) representeert de kans om bij toeval deze gegevens te vinden terwijl H0 waar is: \(P(\overline{x}=84.4|\textrm{H0},n=34)\). In dit geval is die kans \(P\) zeer klein.

Voor de argumentatie is het essentieel dat de gegevens valide zijn en betrouwbaar zijn — juist daarom zijn we uitgebreid ingegaan op validiteit (Hoofdstuk 5) en betrouwbaarheid (Hoofdstuk 12). Als we alles goed gedaan hebben, dan mogen we immers vertrouwen hebben in onze verkregen gegevens. De lage waarschijnlijkheid van de gegevens volgens H0 kunnen we dan redelijkerwijs niet toeschrijven aan fouten in de operationalisatie, of aan meetfouten, of aan andere afwijkingen in de gegevens. De logische conclusie is dan, dat de onwaarschijnlijke uitkomst erop wijst dat de premisse (H0) waarschijnlijk niet waar is: we verwerpen H0; H0 is dus gefalsifieerd. Onze kennis is daarmee toegenomen, omdat we nu op gerechtvaardigde gronden mogen aannemen dat H0 onwaar is (en dus dat H1 waar is).

Indien we H0 verwerpen, op basis van bovenstaande redenering, die weer gebaseerd is op waarschijnlijkheid, dan moeten we wel rekening houden met de kleine kans \(P\) dat het verwerpen van H0 een onterechte beslissing is (Type-I-fout; zie §2.5). Er is immers de kans \(P\) dat we deze data vinden terwijl H0 toch waar is (in dit voorbeeld: terwijl de taalwetenschappers eigenlijk gemiddeld niet anders scoren dan \(\mu=73\)).

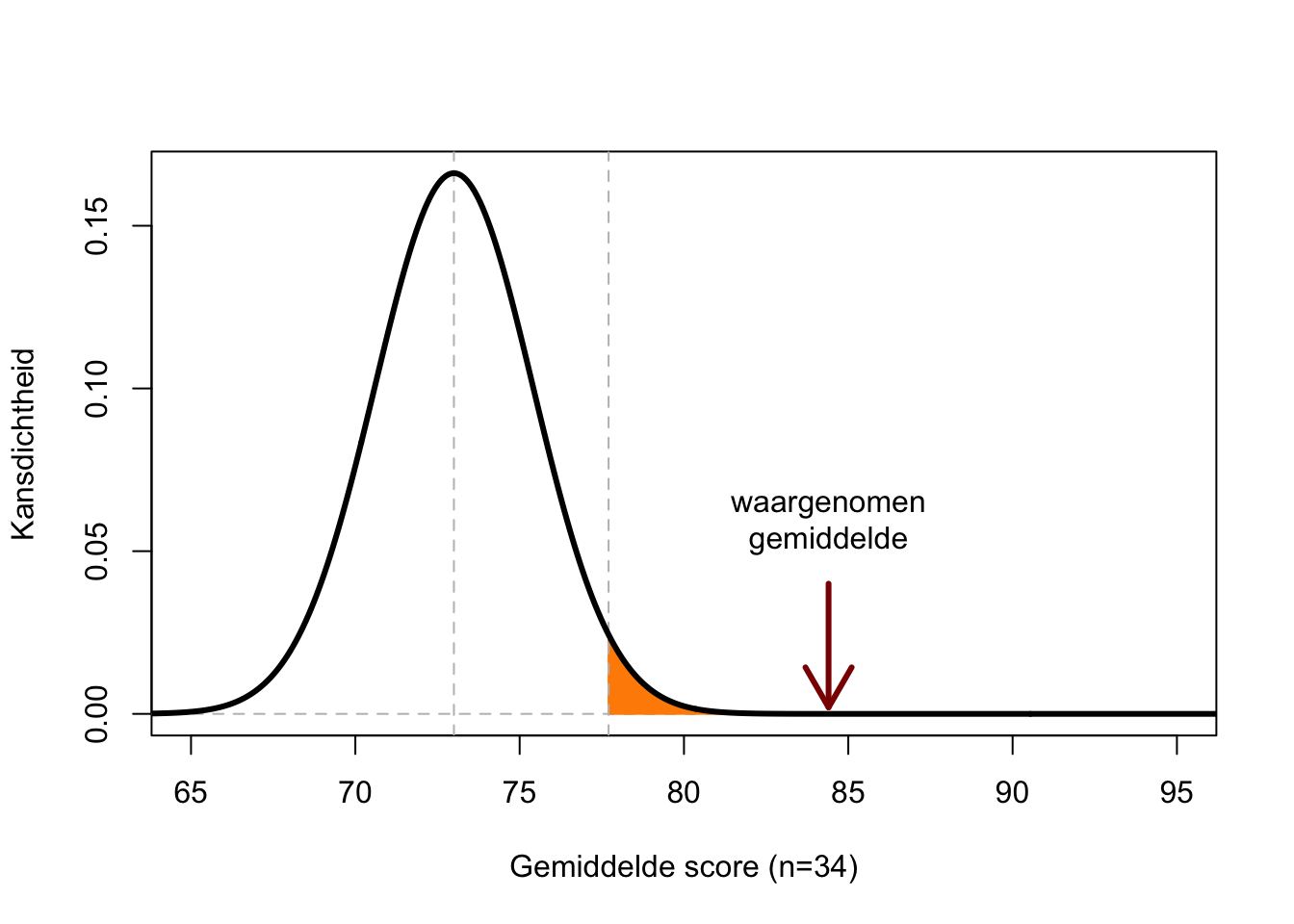
Kansverdeling van de gemiddelde score uit een steekproef (n=34) bij populatiegemiddelde 73 en populatie-s.d. 14. Het gekleurde gebied bestrijkt 5% van de totale oppervlakte onder de curve; uitkomsten langs de X-as van dit gebied hebben dus een kans van ten hoogste 5% om op te treden als H0 waar is.

Figuur 13.1: Kansverdeling van de gemiddelde score uit een steekproef (n=34) bij populatiegemiddelde 73 en populatie-s.d. 14. Het gekleurde gebied bestrijkt 5% van de totale oppervlakte onder de curve; uitkomsten langs de X-as van dit gebied hebben dus een kans van ten hoogste 5% om op te treden als H0 waar is.

Figuur 13.1 toont de kansverdeling van het gemiddelde van de steekproef (\(n=34\)) als H0 waar is. We zien dat de waarde 73 de hoogste kans heeft, maar ook 72 of 74 zijn waarschijnlijke gemiddelde scores volgens H0. Een gemiddelde van 84.4 is echter zeer onwaarschijnlijk, de kans \(P\) op deze gemiddelde score (hoogte van de curve) is bijna nul volgens H0.

De grenswaarde voor \(P\) waarbij we H0 verwerpen, wordt het significantieniveau genoemd, vaak aangeduid met symbool \(\alpha\) (zie §2.5). Onderzoekers gebruiken vaak \(\alpha=.05\), maar soms worden andere grenswaarden gebruikt. In Figuur 13.1 zie je dat de kans op een gemiddelde score van 77.7 of meer een kans heeft van \(P=.05\) of kleiner, volgens H0. Dit is te zien aan de oppervlakte onder de curve. Het gekleurde deel heeft precies een oppervlakte van 0.05 van de totale oppervlakte onder de curve.

De beslissing om H0 wel of niet te verwerpen is gebaseerd op de waarschijnlijkheid \(P\) van de uitkomsten, gegeven H0. De beslissing zou dus ook onjuist kunnen zijn. De bevinding dat \(P < \alpha\) vormt dus geen onomstotelijk bewijs dat H0 onwaar is (en verworpen moet worden); het is ook mogelijk dat H0 toch waar is maar dat het gevonden effect een toevalstreffer was (Type-I-fout). Omgekeerd vormt de bevinding dat \(P > \alpha\) geen sluitend bewijs dat H0 waar is. Er kunnen allerlei andere, plausibele redenen zijn waarom een wel bestaand effect (H0 is onwaar) toch niet goed geobserveerd wordt. Als ik geen vogels hoor zingen, dan betekent dat niet noodzakelijkerwijs dat er echt geen vogels zingen. Meer algemeen: “absence of evidence is not evidence of absence” (Sagan 1996, 121; Alderson 2004). Het is daarom goed om ook altijd de grootte van het gevonden effect of verschil te rapporteren (dit wordt nader uitgelegd in §13.8 hieronder).

Voorbeeld 13.1: Stel H0: ‘vogels zingen niet’. Schrijf tenminste vier redenen op waarom ik geen vogels hoor zingen, zelfs als er wel vogels zingen (H0 is onwaar). Als ik H0 niet verwerp, wat voor type fout maak ik dan?

13.2 \(t\)-toets voor enkele steekproef

De Student \(t\)-toets wordt toegepast om een verschil te kunnen onderzoeken tussen de gemiddelde score van een steekproef, en een a priori veronderstelde waarde van dat gemiddelde. We gebruiken deze toets als de standaarddeviatie \(\sigma\) in de populatie niet bekend is, en dus geschat moet worden uit de steekproef. De gedachtegang is als volgt.

Op grond van het gemiddelde en de standaarddeviatie in de steekproef, en van het (volgens H0) veronderstelde gemiddelde, bepalen we de toetsingsgrootheid \(t\). Als H0 waar is, dan is de waarde \(t=0\) het meest waarschijnlijk. Naarmate het verschil tussen het geobserveerde steekproefgemiddelde en het veronderstelde steekproefgemiddelde groter wordt, neemt \(t\) ook toe. Als de toetsingsgrootheid \(t\) groter is dan een bepaalde grenswaarde \(t*\), dus als \(t>t*\), dan is de kans op deze toetsingsgrootheid, als H0 waar is, erg klein: \(P(t|\textrm{H0}) < \alpha\). De kans om dit resultaat te vinden als H0 waar is, is dan zo gering dat we besluiten H0 te verwerpen (zie §2.5). We spreken dan van een significant verschil: de afwijking tussen het geobserveerde en het verwachte gemiddelde is vermoedelijk niet toevallig.

In het eerdere voorbeeld van de grammaticatoets bij studenten Taalwetenschap (§13.1) hebben we al kennis gemaakt met deze vorm van de \(t\)-toets. Als \(\overline{x}=84.4, s=8.4, n=34\), dan is toetsingsgrootheid \(t=7.9\) volgens formule (13.1) hieronder.

De kansverdeling van toetsingsgrootheid \(t\) onder H0 is bekend; je vindt de grenswaarde \(t^*\) in Bijlage C. Anders gezegd, als de gevonden toetsingsgrootheid \(t\) groter is dan de grenswaarde \(t^*\) die in de tabel staat vermeld, dan is \(P(t|\textrm{H0})<\alpha\). Om de tabel in Bijlage C te kunnen gebruiken moeten we nog een nieuw begrip introduceren, namelijk het aantal vrijheidsgraden. Dat begrip wordt uitgelegd in §13.2.1 hieronder.

Met het aantal vrijheidsgraden kun je in Bijlage C opzoeken welke grenswaarde \(t^*\) nodig is om een bepaalde overschrijdingskans \(p\) te verkrijgen. Laten we opzoeken wat de overschrijdingskans is voor de gevonden toetsingsgrootheid \(t=7.9\). Eerst zoeken we in de linker kolom het aantal vrijheidsgraden (‘d.f.’) op. Als het aantal vrijheidsgraden niet in de tabel voorkomt, dan dienen we voorzichtigheidshalve naar beneden af te ronden, hier naar 30 d.f. Dit aantal bepaalt de regel die voor ons van toepassing is. In de derde kolom staat \(t^*=1.697\). Onze gevonden toetsingsgrootheid \(t=7.9\) is groter dan deze \(t^*=1.697\), dus de overschrijdingskans is kleiner dan de \(p=.05\) die hoort bij de derde kolom. Als we verder naar rechts gaan op dezelfde regel, zien we dat de vermelde \(t^*\) nog toeneemt. Onze gevonden toetsingsgrootheid \(t\) is zelfs nog groter dan \(t^*=3.385\) in de laatste kolom. De overschrijdingskans is dus zelfs nog kleiner dan \(p=.001\) uit de titel van die laatste kolom. (Doorgaans berekent het statistische analyse-programma ook de overschrijdingskans.) We rapporteren het resultaat als volgt:

De gemiddelde score van de studenten Taalwetenschap (lichting 2013) is 84.4 (\(s=8.4\)); dit is significant beter dan het veronderstelde populatie-gemiddelde van 73 (\(t(33)=7.9, p<.001\)).

13.2.1 vrijheidsgraden

Om het concept van vrijheidsgraden uit te leggen, beginnen we met een analogie. Stel dat er drie mogelijke routes zijn om van A naar B te reizen: een kustpad, een bergpad, of een autoweg. Een wandelaar die van A naar B wil reizen, heeft weliswaar drie opties, maar er zijn slechts twee vrijheidsgraden voor de wandelaar: hij of zij hoeft slechts 2 keuzes te maken om te kiezen uit de drie opties. Eerst valt de autoweg af (eerste kies-moment), en dan het bergpad (tweede kies-moment), en de gekozen route langs het kustpad blijft als enige over. Er zijn dus twee keuzes ‘vrij’, om uiteindelijk één van de drie mogelijke routes te kiezen. Als we de twee keuzes weten, dan kunnen we daaruit afleiden welke route gekozen moet zijn.

Nu kijken we naar een student die gemiddeld een \(\overline{x}=7.0\) heeft behaald over de \(N=4\) cursussen van het eerste basispakket van zijn of haar opleiding. Het gemiddelde van \(7.0\) kan op vele manieren tot stand zijn gekomen, bv. \((8,7,7,6)\) of \((5,6,8,9)\). Maar als we van drie cursussen het resultaat weten, èn we weten dat het gemiddelde een 7.0 bedraagt, dan weten we ook wat de waarde van de vierde observatie moet zijn. Die laatste observatie is dus niet meer ‘vrij’ maar wordt nu vastgelegd door de eerste drie observaties, in combinatie met het gemiddelde over de \(N=4\) observaties. We zeggen dan dat je \(N-1\) vrijheidsgraden hebt om dit kenmerk van de steekproef te bepalen, zoals hier het steekproefgemiddelde, of zoals de toetsingsgrootheid \(t\). De vrijheidsgraden worden in het Engels ‘degrees of freedom’ genoemd, vaak afgekort tot ‘d.f.’ (symbool \(\nu\), griekse letter “nu”) .

In de praktijk is het aantal vrijheidsgraden niet moeilijk te bepalen. We geven namelijk bij elke toets aan hoe je de vrijheidsgraden bepaalt — en het aantal d.f. wordt doorgaans ook berekend door de statistische analyse-programma’s die we gebruiken.

Bij de \(t\)-toets voor een enkele steekproef is het aantal vrijheidsgraden het aantal observaties \(N-1\). In het hierboven besproken voorbeeld hebben we dus \(N-1 = 34-1 = 33\) vrijheidsgraden.

13.2.2 formules

\[\begin{equation} t = \frac{ \overline{y}-\mu} { s } \times \sqrt{N} \tag{13.1} \end{equation}\]

13.2.3 aannames

De \(t\)-toets voor een enkele steekproef vereist drie aannames (assumpties) waaraan voldaan moet zijn, om de toets te mogen gebruiken.

  • De gegevens moeten gemeten zijn op intervalniveau (zie hoofdstuk 4).

  • Alle observaties moeten onafhankelijk van elkaar zijn.

  • De scores moeten normaal verdeeld zijn (zie §10.3).

13.2.4 SPSS

De hierboven besproken gegevens zijn te vinden in het bestand data/grammaticatoets2013.csv.

Om onze eerdere hypothese te toetsen, moeten we in SPSS eerst de observaties selecteren van de studenten Taalwetenschap.

Data > Select cases...

Kies If condition is satisfied en druk op knop If... om de condities voor selectie (inclusie) aan te geven.
Selecteer variabele opleiding (sleep naar rechter paneel), kies knop =, en type daarna TW, zodat de hele conditie luidt opleiding = TW.

Daarna kunnen we onze eerdere hypothese toetsen als volgt:

Analyze > Compare Means > One-Sample T Test...

Selecteer variabele score (sleep naar Test variable(s) paneel).
Geef op tegen welke waarde van \(\mu\) getoetst moet worden: geef op als Test Value 73. Bevestig met OK.

De uitvoer bevat zowel beschrijvende statistiek als de resultaten van een tweezijdige \(t\)-toets.

Neem bij het overnemen van die uitvoer goede notitie van de waarschuwing in §13.3 hieronder: SPSS rapporteert alsof p=.000 maar dat is onjuist.

13.2.5 JASP

De hierboven besproken gegevens zijn te vinden in het bestand data/grammaticatoets2013.csv.

Om de eerder besproken hypothese te toetsen, moeten we eerst alleen de observaties van studenten Taalwetenschap selecteren (‘filteren’). Ga daarvoor naar het tabblad met data, en klik op het trechtersymbool (filter) in de cel linksboven. Er verschijnt dan een werkblad waar je je selectie kunt specificeren.
Klik 1x op de variabele opleiding (links), die verspringt dan naar het werkblad. Klik daarna 1x op het symbool = (boven) en plaats de cursor achter het = teken op het werkblad, en typ de twee letters TW (in hoofdletters en zonder aanhalingstekens; exact hetzelfde zoals in de variabele opleiding). Op het werkblad staat nu het selectiecriterium: opleiding = TW.
Klik op de tekst Apply pass-through filter onder het werkblad om dit filter toe te passen. In het tabblad met data zie je nu direct dat de regels van studenten anders dan TW grijs gemaakt zijn. Die regels (observaties) worden niet verder gebruikt.

Klik daarna voor het toetsen van de hypothese in de bovenbalk op:

T-Tests > Classical: One Sample T-Test

Selecteer de variabele score en plaats deze in het veld “Variables”. Zorg dat Student aangevinkt is onder “Tests” en geef bij Test value: op tegen welke waarde van \(\mu\) getoetst moet worden; 73. Onder “Alt.Hypothesis” moet > Test value worden geselecteerd voor een eenzijdige \(t\)-toets (want H1: \(\mu > 73\)). Voor meer inzicht kunnen onder “Additional Statistics” ook Descriptives en Descriptive plots worden aangevinkt. Vink hier ook Effect size aan (zie §13.8 hieronder). Vink als laatste onder het kopje “Assumption checks” ook de optie Normality aan (zie §10.4).

De uitvoer geeft de resultaten van de eenzijdige \(t\)-toets, inclusief effectgrootte. De tabel Assumption Checks geeft de resultaten van de Shapiro-Wilk-toets (die toetst of de afhankelijke variabele normaal verdeeld is). Als dit is aangevinkt wordt ook een tabel met beschrijvende statistiek en een “Descriptive plot” gegeven. Hiermee kun je goed zien waar de waarde \(\mu\) ligt waartegen wordt getoetst ten opzichte van de scores van de studenten Taalwetenschap.

Let op! Voor de toets hebben we een filter aangezet om alleen de studenten Taalwetenschap mee te nemen, en dit filter blijft aan staan als je niks doet. Als je later weer alle observaties wilt gebruiken, maak het filteren dan ongedaan door weer in het data tabblad naar het filter werkblad te gaan en 2x op de prullenbak te klikken. Als het goed gaat staat er “Filter cleared” en worden alle observaties weer zwart in het data tabblad.

13.2.6 R

Onze hierboven besproken hypothese kan worden getoetst met de volgende opdrachten:

gramm2013 <- read.csv( file="data/grammaticatoets2013.csv",header=TRUE)
with( gramm2013,
      t.test( score[opleiding=="TW"], mu=73, alt="greater" ) )
## 
##  One Sample t-test
## 
## data:  score[opleiding == "TW"]
## t = 7.9288, df = 33, p-value = 1.913e-09
## alternative hypothesis: true mean is greater than 73
## 95 percent confidence interval:
##  81.97599      Inf
## sample estimates:
## mean of x 
##  84.41176

De notatie 1.913e-09 moet gelezen worden als het getal \((1.913 \times 10^{-9})\).

13.3 Overschrijdingskans \(p\) is altijd groter dan nul

De overschrijdingskans \(p\) kan heel klein zijn, maar is altijd groter dan nul! In het bovenstaande voorbeeld van de grammaticatoets vonden we \(P=.000000001913\), een heel kleine kans, maar wel groter dan nul. Dat is ook te zien aan de staarten van de bijbehorende kansverdeling, die asymptotisch naderen naar nul (zie Fig.13.1) maar nooit helemaal gelijk aan nul worden. Er is immers altijd een miniem kleine kans dat je een extreme waarde (of een nog extremere waarde) van je toetsingsgrootheid zult vinden in een steekproef — we onderzoeken de steekproef immers juist omdat de uitkomst van de toetsingsgrootheid niet a priori vaststaat.

In SPSS worden de overschrijdingskansen echter afgerond, en kunnen dan in de uitvoer verschijnen als ‘Sig. .000’ oftewel \(p=.000\). Dit is onjuist. De overschrijdingskans of significantie is immers niet gelijk aan nul, maar is afgerond naar nul, en dat is niet hetzelfde. Rapporteer de overschrijdingskans of significantie altijd met de juiste nauwkeurigheid, in dit voorbeeld als \(p<.001\) (zie ook Wright 2003, 125).

13.4 Eenzijdige en tweezijdige toetsen

De procedure die we hierboven hebben besproken geldt voor het éénzijdig toetsen. Dat wil zeggen dat de alternatieve hypothese niet alleen stelt dat de gemiddelden zullen verschillen, maar ook in welke richting dat zal zijn: H1: \(\mu >73\), de studenten Taalwetenschap scoren beter dan het populatiegemiddelde. Als we een verschil zouden vinden in de tegengestelde richting, zeg \(\overline{x}=68\), dan beginnen we niet eens aan statistische toetsing: de H0 blijft zonder meer in stand. Pas als we een verschil vinden in de veronderstelde richting is het zinvol om te inspecteren of dit verschil significant is. Wanneer je nu kijkt naar de afbeelding bij Bijlage C, dan klopt dit ook. De \(p\)-waarde correspondeert met de oppervlakte van het gekleurde gebied.

Indien de alternatieve hypothese H1 de richting van het verschil niet specificeert, dan treedt er een complicatie op. Zowel verschillen in de ene richting als in de andere richting zijn dan immers relevant. We spreken dan van tweezijdig toetsen. Om de tweezijdige overschrijdingskans te berekenen moeten we de \(p\)-waarde uit Bijlage C vermenigvuldigen met \(2\) (omdat we nu kijken naar twee gekleurde gebieden, aan beide zijden van de kansverdeling).

Laten we in het voorbeeld van de grammaticatoets nu tweezijdig toetsen. We operationaliseren de alternatieve hypothese dan als H1: \(\mu \ne 73\). Wederom is \(\overline{x}=73, t=7.9\) met 33 d.f. (afgerond naar 30 d.f.). Bij de eenzijdige overschrijdingskans \(p=.025\) (vierde kolom) vinden we de kritieke grenswaarde \(t^*=2.042\). De tweezijdige overschrijdingskans voor deze grenswaarde is \(2 \times .025 = .05\). Onze gevonden toetsingsgrootheid \(t=7.9\) is groter dan deze \(t^*=2.042\), dus de tweezijdige overschrijdingskans is kleiner dan \(p=2\times.025=.05\). Onze gevonden toetsingsgrootheid \(t\) is zelfs groter dan \(t^*=3.385\) in de laatste kolom, dus de tweezijdige overschrijdingskans is zelfs kleiner dan \(2\times.001\). We kunnen onze tweezijdige toetsing als volgt rapporteren:

De gemiddelde score van de studenten Taalwetenschap (lichting 2013) is 84.4 (\(s=8.4\)); dit verschilt significant van het veronderstelde populatie-gemiddelde van 73 (\(t(33)=7.9, p<.002\)).

In de meeste onderzoeken wordt tweezijdig getoetst; als de richting van de toets niet wordt vermeld dan mag je daarom aannemen dat er tweezijdig is getoetst.

13.5 Betrouwbaarheidsinterval van het gemiddelde

Deze paragraaf gaat dieper in op een onderwerp dat eerder al aan bod kwam in §10.7, en illustreert het betrouwbaarheidsinterval van het gemiddelde met de scores van de grammaticatoets.

Het gemiddelde van de steekproef, \(\overline{x}\), kunnen we beschouwen als een goede schatting van het onbekende gemiddelde in de populatie, \(\mu\). Het betrouwbaarheidsinterval (confidence interval, CI) geeft aan hoeveel vertrouwen we in die schatting mogen hebben, d.w.z., met hoeveel (on)zekerheid het gemiddelde van de steekproef, \(\overline{x}\), overeenkomt met het gemiddelde van de populatie \(\mu\) (Cumming 2012). We kennen zulke foutenmarges ook uit verkiezingsuitslagen, waar ze aangeven hoe zeker de uitslag van de gepeilde steekproef (van respondenten) overeenkomt met de werkelijke verkiezingsuitslag voor de gehele populatie (van kiezers). Een foutenmarge van 2% betekent dat het voor 95% zeker is dat \(x\), het percentage stemmen op een bepaalde partij, zal liggen tussen \((x-2)\)% en \((x+2)\)%.

In ons voorbeeld met 30 d.f. vinden we \(t^*=2.042\) voor 95% betrouwbaarheid. Via formule (10.12) komen we tot het 95% betrouwbaarheidsinterval \((81.5, 87.3)\). Wat betekent dit betrouwbaarheidsinterval? Als we herhaalde steekproeven zouden (kunnen) trekken uit dezelfde populatie van studenten Taalwetenschap, dan zou het betrouwbaarheidsinterval in 95% van die herhaalde steekproeven het werkelijke populatiegemiddelde \(\mu\) bevatten, en in 5% van de herhaalde steekproeven zou het werkelijke populatiegemiddelde buiten het 95% CI vallen. Het CI geeft dus aan “the confidence in the algorithm and [it is] not a statement about a single CI” (https://rpsychologist.com/d3/ci/).

We rapporteren het betrouwbaarheidsinterval als volgt:

De gemiddelde score van de studenten Taalwetenschap (lichting 2013) is 84.4, met 95% betrouwbaarheidsinterval (81.5, 87.3), 33 d.f.

In Figuur 13.2 zie je de resultaten van een computersimulatie om dit te illustreren. Deze figuur is op dezelfde wijze gemaakt als Figuur 10.8 in Hoofdstuk 10 en illustreert hetzelfde punt. We hebben \(100\times\) steekproeven getrokken van scores van studenten Taalwetenschap, met \(\mu=84.4\) en \(\sigma=8.4\) (zie §9.5.2) en \(N=34\). Voor elke steekproef hebben we het 95% betrouwbaarheidsinterval getekend. Voor 95 van de 100 steekproeven valt het populatiegemiddelde \(\mu=84.4\) inderdaad binnen het interval, maar voor 5 van de 100 steekproeven ten onrechte niet (deze zijn gemarkeerd langs de rechterkant). Op de website https://rpsychologist.com/d3/ci/ vind je meer visuele uitleg van het concept van betrouwbaarheidsintervallen.

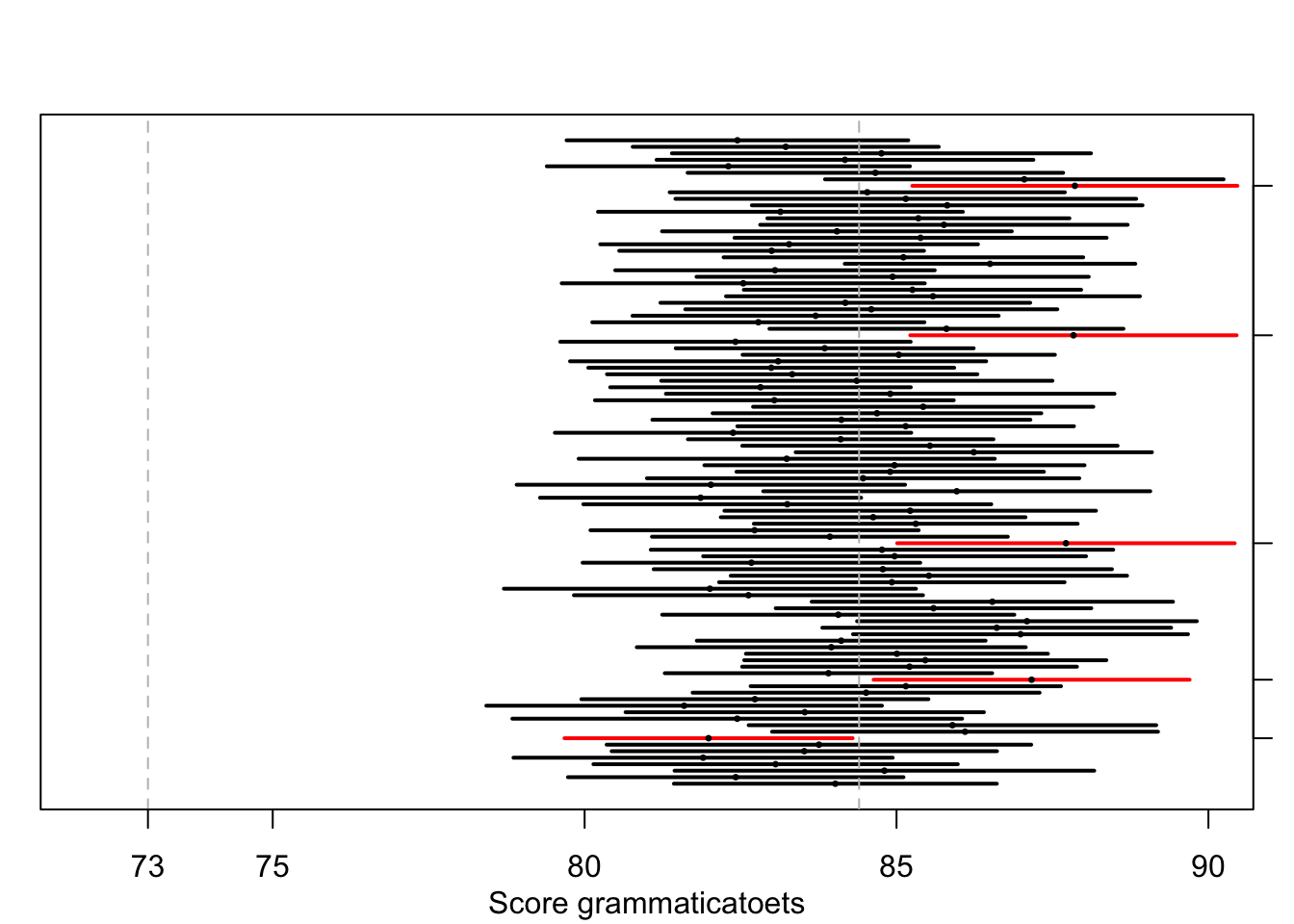
95%-Betrouwbaarheidsintervallen en steekproefgemiddelden, over 100 gesimuleerde steekproeven (n=34) uit een populatie met populatiegemiddelde 84.4, populatie-s.d. 8.4.

Figuur 13.2: 95%-Betrouwbaarheidsintervallen en steekproefgemiddelden, over 100 gesimuleerde steekproeven (n=34) uit een populatie met populatiegemiddelde 84.4, populatie-s.d. 8.4.

Uit formule (13.2) volgt logischerwijze, dat als de standaarddeviatie \(s\) afneemt, en/of als de steekproefgrootte \(N\) toeneemt, het betrouwbaarheidsinterval dan kleiner wordt, m.a.w., we kunnen er meer vertrouwen in hebben dat het geobserveerde gemiddelde van de steekproef dicht bij het onbekende gemiddelde van de populatie ligt.

13.5.1 formules

Het tweezijdige betrouwbaarheidsinterval voor \(B\)% betrouwbaarheid voor een populatie-gemiddelde \(\mu\) is \[\begin{equation} \overline{y} \pm t^*_{1-B,N-1} \times \frac{s}{\sqrt{N}} \tag{13.2} \end{equation}\] (zie ook eerdere formule (10.12)).

13.5.2 SPSS

Analyze > Descriptive Statistics > Explore...

Selecteer afhankelijke variabele (sleep naar Dependent List paneel).
Kies knop Statistics en vink aan Descriptives met Confidence Interval 95%.
Bevestig met Continue en met OK.
De uitvoer bevat meerdere beschrijvende statistische maten, waaronder nu ook het 95% betrouwbaarheidsinterval van het gemiddelde.

13.5.3 JASP

In JASP kun je het betrouwsbaarheidsinterval van het gemiddelde aanvragen bij een \(t\)-toets. We voeren dus wederom een \(t\)-toets uit en vinden het betrouwbaarheidsinterval van het gemiddelde in de uitvoer.

Zorg dat het filter aanstaat zodat alleen de observaties van studenten Taalwetenschap geselecteerd zijn (zie §13.2.5).

Klik daarna in de bovenbalk op:

T-Tests > Classical: One Sample T-Test

Selecteer de variabele score en plaats deze in het veld “Variables”. Zorg dat Student aangevinkt is onder “Tests” en laat Test value: op 0 staan. Vink onder “Additional Statistics” Location parameter aan en ook Confidence interval. Hier kun je zelf het betrouwbaarheidsniveau opgeven; dit staat standaard op 95%.

De uitvoer geeft nu als ‘Mean Difference’ het gemiddelde aan (want er wordt vergeleken met 0; dat is de ‘Test value’). In dezelfde tabel zie je het ‘95% CI for Mean Difference’, wat in dit geval dus het betrouwbaarheidsinterval van het gemiddelde is.

13.5.4 R

R vermeldt het betrouwbaarheidsinterval van het gemiddelde (met een zelf op te geven betrouwbaarheidsniveau) bij een \(t\)-toets. We voeren dus wederom een \(t\)-toets uit en vinden het betrouwbaarheidsinterval van het gemiddelde in de uitvoer.

with( gramm2013, t.test( score[opleiding=="TW"] ) )
## 
##  One Sample t-test
## 
## data:  score[opleiding == "TW"]
## t = 58.649, df = 33, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  81.48354 87.33999
## sample estimates:
## mean of x 
##  84.41176

13.6 \(t\)-toets voor twee onafhankelijke steekproeven

De Student \(t\)-toets wordt toegepast om een verschil te kunnen onderzoeken tussen de gemiddelde scores van twee onafhankelijke steekproeven, bv van vergelijkbare jongens en meisjes. Op grond van de gemiddelden en de standaarddeviaties van de twee steekproeven bepalen we de toetsingsgrootheid \(t\). Als H0 waar is, dan is de waarde \(t=0\) het meest waarschijnlijk. Naarmate het verschil tussen de twee gemiddelden groter wordt, neemt \(t\) ook toe. Wederom verwerpen we H0 indien \(t>t^*\) voor het gekozen significantieniveau \(\alpha\).

Als eerste voorbeeld nemen we een onderzoek naar de omvang van de productieve woordenschat bij Zweedse meisjes en jongens van 18 maanden oud (Andersson et al. 2011). We onderzoeken de veronderstelling dat de woordenschat van meisjes verschilt van die van jongens, d.w.z. H1: \(\mu_m \ne \mu_j\). We kunnen niet a priori aannemen dat een eventueel verschil slechts één richting op kan gaan; we toetsen daarom tweezijdig, zoals al blijkt uit H1. De bijbehorende nul-hypothese die we toetsen is H0: \(\mu_m = \mu_j\). In dit onderzoek werd de woordenschat geschat op grond van vragenlijsten aan de ouders van de kinderen in de steekproeven. Deelnemers waren (ouders van) \(n_1=123\) meisjes en \(n_2=129\) jongens, allen 18 maanden oud. Uit de resultaten blijkt dat de meisjes een gemiddelde woordenschat hebben van \(\overline{x_1}=95\) woorden (\(s_1=82\)), en voor de jongens is dat \(\overline{x_2}=85\) woorden (\(s_2=98\)). Met deze gegevens bepalen we de toetsingsgrootheid \(t\) volgens formule (13.4), resulterend in \(t=0.88\) met 122 d.f. De bijbehorende kritieke grenswaarde \(t^*\) zoeken we wederom op in Bijlage C. In de regel voor 100 d.f. (na afronding naar beneden) vinden we \(t^*=1.984\) in de vierde kolom. Voor tweezijdige toetsing moeten we de overschrijdingskans behorend bij deze kolom verdubbelen (zie §13.4), resulterend in \(p=.05\). De gevonden toetsingsgrootheid \(t < t^*\), dus \(p>.05\). We besluiten om H0 niet te verwerpen, en rapporteren dat als volgt:

De gemiddelde productieve woordenschat van Zweedse kinderen van 18 maanden oud verschilt nauwelijks tussen meisjes en jongens (\(t(122)=0.88, p>.4\)). Meisjes produceren gemiddeld 95 verschillende woorden (\(s=82\)), en jongens gemiddeld 85 verschillende woorden (\(s=98\)).

Als tweede voorbeeld nemen we een onderzoek naar het spreektempo van twee groepen sprekers, nl. afkomstig uit het Westen (eerste groep) en uit het Noorden (tweede groep) van Nederland. De spreeksnelheid wordt hier uitgedrukt als de gemiddelde duur van een gesproken lettergreep, gemiddeld over een interview van ca 15 minuten (zie voorbeeld 15.1). We onderzoeken H0: \(\mu_W = \mu_N\) met tweezijdige toetsing. Uit de resultaten blijkt dat de westerlingen (\(n=20\)) een gemiddelde lettergreepduur hebben van \(\overline{x_W}=0.235\) s (\(s=0.028\)), en voor de noorderlingen (ook \(n=20\)) is dat \(\overline{x_N}=0.269\) s (\(s=0.029\)). Met deze gegevens bepalen we wederom de toetsingsgrootheid \(t\) volgens formule (13.4), resulterend in \(t=-3.76\) met 38 d.f. De bijbehorende kritieke grenswaarde \(t^*\) zoeken we wederom op in Bijlage C. De juiste d.f. zijn niet in de tabel vermeld, dus ronden we naar beneden af (d.i. in conservatieve richting) naar 30 d.f. In die regel vinden we \(t^*=2.042\) in de vierde kolom. Voor tweezijdige toetsing moeten we de overschrijdingskans behorend bij deze kolom verdubbelen (zie §13.4), resulterend in \(p=.05\). De gevonden toetsingsgrootheid \(t < t^*\), dus \(p<.05\). We besluiten daarom om H0 wel te verwerpen, en rapporteren dat als volgt:

De gemiddelde duur van een lettergreep gesproken door een spreker uit het westen van Nederland is \(0.235\) seconde (\(s=0.03\)). Dit is significant korter dan bij sprekers uit het Noorden van Nederland (\(\overline{x}=0.269\) s, \(s=0.03\)) (\(t(38)=-3.76, p<.05\)). In de onderzochte opnames uit 1999 praten de sprekers uit het Westen dus sneller dan die uit het Noorden van Nederland.

13.6.1 aannames

De Student \(t\)-toets voor twee onafhankelijke steekproeven vereist vier aannames (of assumpties) waaraan voldaan moet zijn, om de toets te mogen gebruiken.

  • De gegevens moeten gemeten zijn op intervalniveau (zie §4.4).

  • Alle observaties moeten onafhankelijk van elkaar zijn.

  • De scores moeten normaal verdeeld zijnin beide groepen (zie §10.4).

  • De variantie van de scores moet gelijk zijn in beide steekproeven. Schending van deze aanname is ernstiger naarmate de twee steekproeven meer in grootte verschillen. Het is daarom verstandig om te werken met even grote, en liefst niet te kleine steekproeven. Als de steekproeven even groot zijn dan is het schenden van deze aanname van gelijke varianties niet zo ernstig. Zie ook §13.6.2 direct hieronder.

13.6.2 formules

13.6.2.1 toetsingsgrootheid

Voor de berekening van de toetsingsgrootheid \(t\) zijn verschillende formules in gebruik.

Indien de steekproeven ongeveer gelijke variantie hebben, dan gebruiken we eerst de “pooled standard deviation” \(s_p\) als tussenstap. De beide standaarddeviaties van de twee steekproeven worden daarin gewogen naar hun steekproefomvang. \[\begin{equation} s_p = \sqrt{ \frac{(n_1-1) s^2_1 + (n_2-1) s^2_2} {n_1+n_2-2} } \tag{13.3} \end{equation}\] Vervolgens \[\begin{equation} \tag{13.4} t = \frac{ \overline{x_1}-\overline{x_2} } { s_p \sqrt{\frac{1}{n_1}+\frac{1}{n_2}} } \end{equation}\]

Indien de steekproeven niet gelijke varianties hebben, en de vierde aanname hierboven dus is geschonden, dan wordt Welch’s benadering gebruikt: \[\begin{equation} \tag{13.5} s_{\textrm{WS}} = \sqrt{\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2} } \end{equation}\] Vervolgens \[\begin{equation} \tag{13.6} t = \frac{ \overline{x_1}-\overline{x_2} } { s_{\textrm{WS}} } \end{equation}\]

13.6.2.2 vrijheidsgraden

Meestal wordt de \(t-toets\) uitgevoerd door een computerprogramma. Daarbij wordt dan meestal de volgende benadering gebruikt van de vrijheidsgraden (\(\nu\), zie §13.2.1). Eerst worden \(g_1=s^2_1/n_1\) en \(g_2=s^2_2/n_2\) berekend. Het aantal vrijheidsgraden van \(t\) is dan \[\begin{equation} \tag{13.7} \nu_\textrm{WS} = \frac {(g_1+g_2)^2} {g^2_1/(n_1-1) + g^2_2/(n_2-1)} \end{equation}\]

Het aantal vrijheidsgraden volgens deze benadering heeft als liberale bovengrens \((n_1+n_2-2)\), en als conservatieve ondergrens de kleinste van \((n_1-1)\) of \((n_2-1)\). Je kunt dus ook altijd deze conservatieve ondergrens gebruiken. Indien de twee groepen ongeveer dezelfde variantie hebben (d.i. \(s_1 \approx s_2\)), dan kan je ook de liberale bovengrens gebruiken.

Voor het tweede voorbeeld hierboven geeft de benadering van formule (13.7) de schatting van \(37.99 \approx 38\) d.f. De conservatieve ondergrens is \(n_1-1 = n_2-1 = 19\). De liberale bovengrens is \(n_1+n_2 -2 = 38\). (In de tabel met kritische waarden \(t*\), in Bijlage C, is het meestal raadzaam om de regel te gebruiken met de eerstvolgende kleinere waarde voor het aantal vrijheidsgraden.)

13.6.3 SPSS

Het tweede bovenstaande voorbeeld wordt hier uitgewerkt.

Analyze > Compare Means > Independent-Samples T Test

Sleep de afhankelijke variabele syldur naar paneel Test Variable(s). Sleep de onafhankelijke variabele region naar paneel Grouping Variable. Definieer de twee groepen: waarde W voor regio groep 1 en waarde N voor regrio groep 2. Bevestig met Continue en OK.

Zoals je hierboven kon zien, is de berekening van de \(t\)-toets afhankelijk van het antwoord op de vraag of de standaarddeviaties van de twee groepen ongeveer gelijk zijn. SPSS lost dat zeer onhandig op: je krijgt alle relevante uitvoer te zien, en moet daar zelf een keuze uit maken.

13.6.3.1 Test for equality of variances

Met Levene’s test wordt onderzocht H0: \(s^2_1 = s^2_2\), d.w.z. of de varianties (en daarmee de standaarddeviaties) van de twee groepen gelijk zijn. Als je een kleine waarde vindt voor de toetsingsgrootheid \(F\), en een \(p>.05\), dan hoef je deze H0 niet te verwerpen. Je mag dan aannemen dat de varianties gelijk zijn. Als je een grote waarde vindt voor \(F\), met \(p<.05\), dan dien je deze H0 wel te verwerpen, en je mag niet aannemen dat de varianties van de twee groepen gelijk zijn. Gebruik en rapporteer de juiste t-toets uit de uitvoer.

13.6.3.2 Test for equality of means

Afhankelijk van deze uitkomst van Levene’s test moet je de eerste of de tweede regel gebruiken van de uitvoer van de Independent-Samples Test (een toets die onderzoekt of de gemiddelden van de twee groepen gelijk zijn). In dit voorbeeld zijn de varianties ongeveer gelijk, zoals de Levene’s test ook aangeeft. We gebruiken dus de eerste regel van de uitvoer, en rapporteren \(t(38)=-3.76, p=.001\).

13.6.4 JASP

Het tweede bovenstaande voorbeeld wordt hier uitgewerkt: het spreektempo van sprekers uit het Westen en Noorden van Nederland wordt vergeleken.

13.6.4.1 voorbereiding

Hiervoor moeten we eerst zorgen dat alleen de regio’s Noord en West zijn geselecteerd. Dit doe je door in het data tabblad op de variabele-naam region te klikken. Er opent een veld met daarin de verschillende waardes (‘Values’; in dit geval regio’s) van de nominale variabele. Je kunt hier bepaalde waardes (regio’s) van de nominale variabele tijdelijk filteren. In de kolom “Filter” staan standaard alleen maar vinkjes, wat betekent dat alle observaties worden meegenomen. Klik op de vinkjes bij de waardes (regio’s) die je tijdelijk niet mee wilt nemen, S (Zuid) en M (Midden), zodat het kruizen worden. In het data tabblad zie je de bijbehorende observaties dan grijs worden. Zorg dus dat er alleen nog maar bij N (Noord) en W (West) een vinkje staat om alleen de observaties van sprekers uit het Westen en Noorden van Nederland te selecteren.
(Vergeet niet later de kruizen weer terug te veranderen in vinkjes als je wel weer alle observaties wilt meenemen!).

13.6.4.2 t-toets

Klik na het filteren van de goede regio’s in de bovenbalk op:

T-Tests > Classical: Independent Samples T-Test

Selecteer de variabele syldur en plaats deze in het veld “Variables”. Plaats de variabele region in het veld “Grouping Variable”. Als een variabele meer dan twee groepen bevat geeft JASP aan dat er een probleem is (je kunt immers maar twee groepen vergelijken); daarom filteren we hierboven zo dat we alleen Noord en West meenemen in de variabele region.
Zorg dat Student aangevinkt is onder “Tests” en onder “Alt.Hypothesis” moet de eerste optie (de groepen zijn niet hetzelfde) worden aangevinkt voor een tweezijdige \(t\)-toets. Voor meer inzicht kunnen onder “Additional Statistics” ook Descriptives en Descriptive plots worden aangevinkt. Vink hier ook Effect size (Cohen’s d) aan (zie §13.8 hieronder).
Vink onder het kopje “Assumption checks” ook de optie Normality aan (§13.6.1, derde assumptie, zie ook §10.4) en eveneens Equality of variances (§13.6.1, vierde assumptie).

De uitvoer geeft de resultaten van de tweezijdige \(t\)-toets, inclusief effectgrootte.

Onder Assumption Checks vind je de resultaten van de Shapiro-Wilk-toets, die toetst of de afhankelijke variabele normaal verdeeld is in beide groepen. Ook zie je de tabel ‘Test of Equality of Variances (Levene’s)’. Met Levene’s test wordt onderzocht H0: \(s^2_1 = s^2_2\), d.w.z. of de varianties (en daarmee de standaarddeviaties) van de twee groepen gelijk of ongelijk zijn (zie §13.6.2 hierboven). Als je een kleine waarde vindt voor de toetsingsgrootheid \(F\), en een \(p>.05\), dan hoef je deze H0 niet te verwerpen. Je mag dan aannemen dat de varianties wel gelijk zijn. Gebruik en rapporteer dan de Student versie van de \(t\)-toets (die is hierboven gekozen onder “Tests”). Als je een grote waarde vindt voor \(F\), met \(p<.05\), dan dien je deze H0 wel te verwerpen, en je mag dan niet aannemen dat de varianties van de twee groepen gelijk zijn. Kies dan onder het kopje “Tests” de optie Welch, en gebruik en rapporteer dan de Welch versie van de t-toets.

In dit voorbeeld geven de toetsen voor normaliteit en voor gelijke varianties geen significante resultaten. Dat betekent dat aan de derde en vierde bovengenoemde assumptie is voldaan; we gebruiken en rapporteren dan de Student \(t\)-toets: \(t(38)=3.76, p<.001, d=1.2\).

Als dit is aangevinkt wordt als laatste in de uitvoer een tabel met beschrijvende statistiek en een “Descriptive plot” gegeven. Hiermee kun je goed zien hoe de scores van de twee groepen van elkaar verschillen.

13.6.5 R

require(hqmisc)
data(talkers)
with(talkers, t.test( syldur[region=="W"], syldur[region=="N"], 
            paired=F, var.equal=T ) )
## 
##  Two Sample t-test
## 
## data:  syldur[region == "W"] and syldur[region == "N"]
## t = -3.7649, df = 38, p-value = 0.0005634
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.0519895 -0.0156305
## sample estimates:
## mean of x mean of y 
##   0.23490   0.26871

13.7 \(t\)-toets voor gepaarde waarnemingen

De Student \(t\)-toets wordt ook toegepast om een verschil te onderzoeken tussen de gemiddelden van twee afhankelijke of gepaarde waarnemingen. Daarvan is sprake als we slechts één steekproef trekken (zie hoofdstuk 7), en van de leden van deze steekproef vervolgens twee observaties verzamelen, nl. één observatie onder elk van beide condities. De twee observaties zijn dan gepaard, d.w.z. aan elkaar gerelateerd, en deze observaties zijn dus niet onafhankelijk (want afkomstig van hetzelfde lid van de steekproef). Eén van de assumpties van de \(t\)-toets is daarmee geschonden.

Als voorbeeld nemen we een denkbeeldig onderzoek naar het gebruik van U of je als aanspreekvorm op een website. De onderzoeker maakt twee versies van een webpagina, de ene met U en de andere met je. Elke respondent moet beide versies beoordelen op een schaal van 1 tot 10. (Om redenen van validiteit wordt de volgorde van de twee versies gevarieerd tussen respondenten; de volgorde waarin de pagina’s beoordeeld zijn, kan dus geen invloed hebben op de totaalscore per conditie.) In Tabel 13.1 zijn de oordelen van \(N=10\) respondenten samengevat.

Tabel 13.1: Fictieve oordelen over een webpagina met U of je als aanspreekvorm, door \(N=10\) respondenten.
id conditie U conditie je \(D\)
1 8 9 -1
2 5 6 -1
3 6 9 -3
4 6 8 -2
5 5 8 -3
6 4 6 -2
7 4 8 -4
8 7 10 -3
9 7 9 -2
10 6 7 -1
\(\overline{D}\)=-2.2

Het paar van observaties voor het \(i\)-de lid van de steekproef heeft een verschil-score die we kunnen schrijven als: \(D_i = x_{1i} - x_{2i}\) waarbij \(x_{1i}\) de score is van de afhankelijke variabele is voor het \(i\)-de lid van de steekproef in conditie 1, en \(x_{2i}\) de score voor het \(i\)-de lid voor conditie 2. Deze verschilscore is ook vermeld in Tabel 13.1.

Deze verschilscore \(D\) wordt vervolgens eigenlijk geanalyseerd met de eerder besproken \(t\)-toets voor één enkele steekproef (zie §13.2), waarbij H0: \(\mu_D=0\), d.w.z. volgens H0 is er geen verschil tussen condities. We berekenen het gemiddelde van de verschilscore, \(\overline{D}\), en de standaarddeviatie van de verschilscore, \(s_{D}\), op de gebruikelijke wijze (zie §9.5.2). We gebruiken dit gemiddelde en deze standaarddeviatie om de toetsingsgrootheid \(t\) te berekenen, via formule (13.8), met \((N-1)\) vrijheidsgraden. Tenslotte gebruiken we weer Bijlage C om de grenswaarde \(t^*\) te bepalen, en daarmee de overschrijdingskans \(p\) voor de gevonden waarde van de steekproefgrootheid \(t\) onder H0.

Voor het bovengenoemde voorbeeld met U of je als aanspreekvorm vinden we aldus \(\overline{D}=-2.2\) en \(s_D=1.0\). Als we dit invullen in formule (13.8) vinden we \(t=-6.74\) met \(N-1=9\) d.f. De bijbehorende kritieke grenswaarde \(t^*\) zoeken we wederom op in Bijlage C. Daarbij negeren we het teken van \(t\), omdat de kansverdeling van \(t\) immers symmetrisch is. In de regel voor 9 d.f. vinden we \(t^*=4.297\) in de laatste kolom. Voor tweezijdige toetsing moeten we de overschrijdingskans behorend bij deze kolom verdubbelen (zie §13.4), resulterend in \(p=.002\). De gevonden toetsingsgrootheid \(t > t^*\), dus \(p<.002\). We besluiten om H0 wel te verwerpen, en rapporteren dat als volgt:

Het oordeel van \(N=10\) respondenten over de pagina met U als aanspreekvorm is gemiddeld 2.2 punten lager dan hun oordeel over de vergelijkbare pagina met je als aanspreekvorm; dit is een significant verschil (\(t(9)=-6.74, p<.002\)).

13.7.1 aannames

De \(t\)-toets voor gepaarde waarnemingen binnen een enkele steekproef vereist drie aannames (assumpties) waaraan voldaan moet zijn, om deze toets te mogen gebruiken.

  • De gegevens moeten gemeten zijn op intervalniveau (zie §4.4).

  • Alle paren van observaties moeten onafhankelijk van elkaar zijn.

  • De verschilscores \(D\) moeten normaal verdeeld zijn (zie §10.4); als het aantal paren van waarnemingen in de steekproef echter groter is dan ca 30 dan is de \(t\)-toets doorgaans goed bruikbaar.

13.7.2 formules

\[\begin{equation} \tag{13.8} t = \frac{ \overline{D}-\mu_D} { s_D } \times \sqrt{N} \end{equation}\]

13.7.3 SPSS

De gegevens voor het bovenstaande voorbeeld zijn te vinden in bestand data/ujedata.csv.

Analyze > Compare Means > Paired-Samples T Test

Sleep eerste afhankelijke variabele cond.u naar paneel Paired Variables onder Variable1, en sleep tweede variabele cond.je naar zelfde paneel onder Variable2. Bevestig met OK.

13.7.4 JASP

Het bovenstaande voorbeeld wordt hier uitgewerkt. De gegevens zijn te vinden in bestand data/ujedata.csv.

Klik in de bovenbalk op:

T-Tests > Classical: Paired Samples T-Test

Selecteer de variabelen cond.u en cond.je in het veld “Variable pairs”. Ze komen naast elkaar te staan, want deze twee condities ga je met elkaar vergelijken.
Zorg dat Student aangevinkt is onder “Tests” en onder “Alt.Hypothesis” moet de eerste optie (de metingen zijn niet hetzelfde) worden aangevinkt voor een tweezijdige \(t\)-toets. Voor meer inzicht kunnen onder “Additional Statistics” ook Descriptives en Descriptive plots worden aangevinkt. Vink hier ook Effect size (Cohen’s d) aan (zie §13.8 hieronder). Vink als laatste onder het kopje “Assumption checks” ook de optie Normality aan (zie §10.4).

De uitvoer geeft de resultaten van de tweezijdige \(t\)-toets, inclusief effectgrootte. Je ziet onder ‘Measure 1’ en ‘Measure 2’ in de tabel dat de verschilscore (\(cond.u - cond.je\)) wordt geanalyseerd.
Onder Assumption Checks vind je de resultaten van de Shapiro-Wilk-toets, die toetst of de verschilscores (\(cond.u - cond.je\)) normaal verdeeld zijn.
Als dit is aangevinkt wordt als laatste in de uitvoer een tabel met beschrijvende statistiek en een “Descriptive plot” gegeven. Hiermee kun je goed zien hoe de twee condities van elkaar verschillen in scores.

13.7.5 R

De gegevens voor het bovenstaande voorbeeld zijn te vinden in bestand data/ujedata.csv.

ujedata <- read.table( file="data/ujedata.csv", header=TRUE, sep=";" )
with(ujedata, t.test( cond.u, cond.je, paired=TRUE ) )
## 
##  Paired t-test
## 
## data:  cond.u and cond.je
## t = -6.7361, df = 9, p-value = 8.498e-05
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  -2.938817 -1.461183
## sample estimates:
## mean difference 
##            -2.2

13.8 Effectgrootte

Tot nu toe zijn we vooral ingegaan op toetsing als een binaire beslissing om H0 wel of niet te verwerpen, in het licht van de observaties. Maar het is daarnaast ook van groot belang om te weten hoe groot het geobserveerde effect eigenlijk is: de effectgrootte (Eng. ‘effect size’, ‘ES’) (Cohen 1988; B. Thompson 2002; Nakagawa and Cuthill 2007).

In formules (13.1) en (13.8) komt tot uiting dat de toetsingsgrootheid \(t\) groter wordt, naarmate het effect groter wordt, d.w.z. bij een groter verschil \((\overline{x}-\mu)\) of \((\overline{x_1}-\overline{x_2})\) of \((\overline{D}-\mu_D)\)], en/of naarmate de steekproef groter wordt. Kort gezegd (Rosenthal and Rosnow 2008, 338, formule 11.10): \[\begin{equation} \tag{13.9} \textrm{significance of test} = \textrm{size of effect} \times \textrm{size of study} \end{equation}\]

Dat houdt in dat een klein, en mogelijk triviaal effect, ook statistisch significant kan zijn als de steekproef maar groot genoeg is. Omgekeerd kan een heel groot effect goed vastgesteld worden op basis van een zeer kleine steekproef.

Voorbeeld 13.2: In een onderzoek naar de levensduur van overleden 50+-ers uit Oostenrijk en Denemarken (Doblhammer 1999) bleek dat de levensduur verschilt met de geboorteweek, vermoedelijk omdat babies uit “zomerzwangerschappen” gemiddeld iets gezonder zijn (of waren) dan die uit “winterzwangerschappen”. In dit onderzoek waren de verschillen in levensduur zeer gering (\(\pm 0.30\) jaar in Oostenrijk, \(\pm 0.15\) jaar in Denemarken), maar het aantal observaties (overledenen) was zeer groot.

Daarentegen is het verschil in lichaamslengte tussen dwergen (korter dan 1.5 m) en reuzen (langer dan 2.0 m) zo groot dat het verschil empirisch goed kan worden vastgesteld op basis van slechts \(n=2\) in elke groep.

In ons onderzoek zijn we vooral geïnteresseerd in belangrijke verschillen, d.w.z. doorgaans grote verschillen. We moeten beseffen dat onderzoek ook kosten met zich meebrengt in termen van geld, tijd, inspanning, privacy, en verlies van onbevangenheid voor ander onderzoek (zie hoofdstuk 3). We willen dus niet nodeloos onderzoek doen naar triviale effecten. Een onderzoeker dient daarom vooraf te bepalen wat het kleinste effect is dat hij/zij wil kunnen opsporen, bv. 1 punt verschil in de score van de grammaticatoets. Verschillen kleiner dan 1 punt worden dan beschouwd als triviaal, en verschillen groter dan 1 punt als potentieel interessant.

Ook is het van belang om de gevonden effectgrootte te vermelden bij de resultaten van een onderzoek, om lezers en latere onderzoekers van dienst te zijn. In sommige wetenschappelijke tijdschriften is het zelfs verplicht om effectgrootte te rapporteren. Dat kan overigens ook in de vorm van een betrouwbaarheidsinterval van het gemiddelde (zie 13.5), omdat we deze betrouwbaarheidsintervallen en effectgroottes in elkaar kunnen omrekenen.

De ruwe effectgrootte is eenvoudigweg het verschil \(D\) in gemiddelden tussen twee groepen, of tussen twee condities, uitgedrukt in eenheden van de ruwe score. In §13.6 vonden we zo een verschil in woordenschat van \(D=95-85=10\) tussen jongens en meisjes.

Meestal gebruiken we echter de gestandaardiseerde effectgrootte (zie formules hieronder), waarbij we rekening houden met de spreiding in de observaties, bijv in de vorm van “pooled standard deviation” \(s_p\) 30. We vinden zo een gestandaardiseerde effectgrootte van \[\begin{equation} \tag{13.10} d = \frac{ \overline{x_1}-\overline{x_2} } {s_p} = \frac{10}{90.5} = 0.11 \end{equation}\] In het eerste voorbeeld hierboven is de gestandaardiseerde effectgrootte van het verschil in woordenschat tussen meisjes en jongens dus 0.11. In dit geval is het verschil tussen de groepen gering ten opzichte van de spreiding binnen de groepen — de kans dat een willekeurig gekozen meisje een grotere woordenschat heeft dan een willekeurig gekozen jongen, is slechts 0.53 (McGraw and Wong 1992), en dat is nauwelijks beter dan de kans van 0.50 die we verwachten volgens H0. Dat dit zeer kleine effect niet significant is (zie §13.6) wekt dan ook geen verbazing. We zouden de effectgrootte en significantie als volgt kunnen rapporteren:

De gemiddelde productieve woordenschat van Zweedse kinderen van 18 maanden oud verschilt nauwelijks tussen meisjes en jongens. Meisjes produceren gemiddeld 95 verschillende woorden (\(s=82\)), en jongens gemiddeld 85 verschillende woorden (\(s=98\)). Het verschil is zeer klein (\(d=0.11)\) en niet significant (\(t(122)=0.88, p>.4\)).

In het tweede voorbeeld hierboven is de gestandaardiseerde effectgrootte van het verschil in duren van lettergrepen ongeveer \((0.235-0.269)/0.029 \approx 1.15\). Dit relatief grote effect kunnen we als volgt rapporteren:

De gemiddelde duur van een lettergreep gesproken door een spreker uit het westen van Nederland is \(0.235\) seconde (\(s=0.03\)). Dit is aanzienlijk korter dan bij sprekers uit het Noorden van Nederland (\(\overline{x}=0.269\) s, \(s=0.03\)). Het verschil is ca. 10%; dit verschil is zeer groot (\(d=-1.15\)) en significant (\(t(38)=-3.76, p<.05\)). In de onderzochte opnames uit 1999 praten de sprekers uit het Westen dus aanzienlijk sneller dan die uit het Noorden van Nederland.

Als \(d\) ligt rond 0.01 spreken we van een zeer klein effect (Sawilowsky 2009). Als \(d\) ligt rond 0.2 spreken we van een klein effect. Een effectgrootte \(d\) rond 0.5 noemen we een middelmatig (medium) effect, en een \(d\) rond 0.8 of groter noemen we een groot effect (Cohen 1988; Rosenthal and Rosnow 2008). Als \(d\) ligt rond 1.2 dan spreken we van een zeer groot effect, en als \(d\) ligt rond 2.0 dan noemen we dat een ‘enorm’ of ‘reusachtig’ effect (‘huge,’ Sawilowsky 2009).

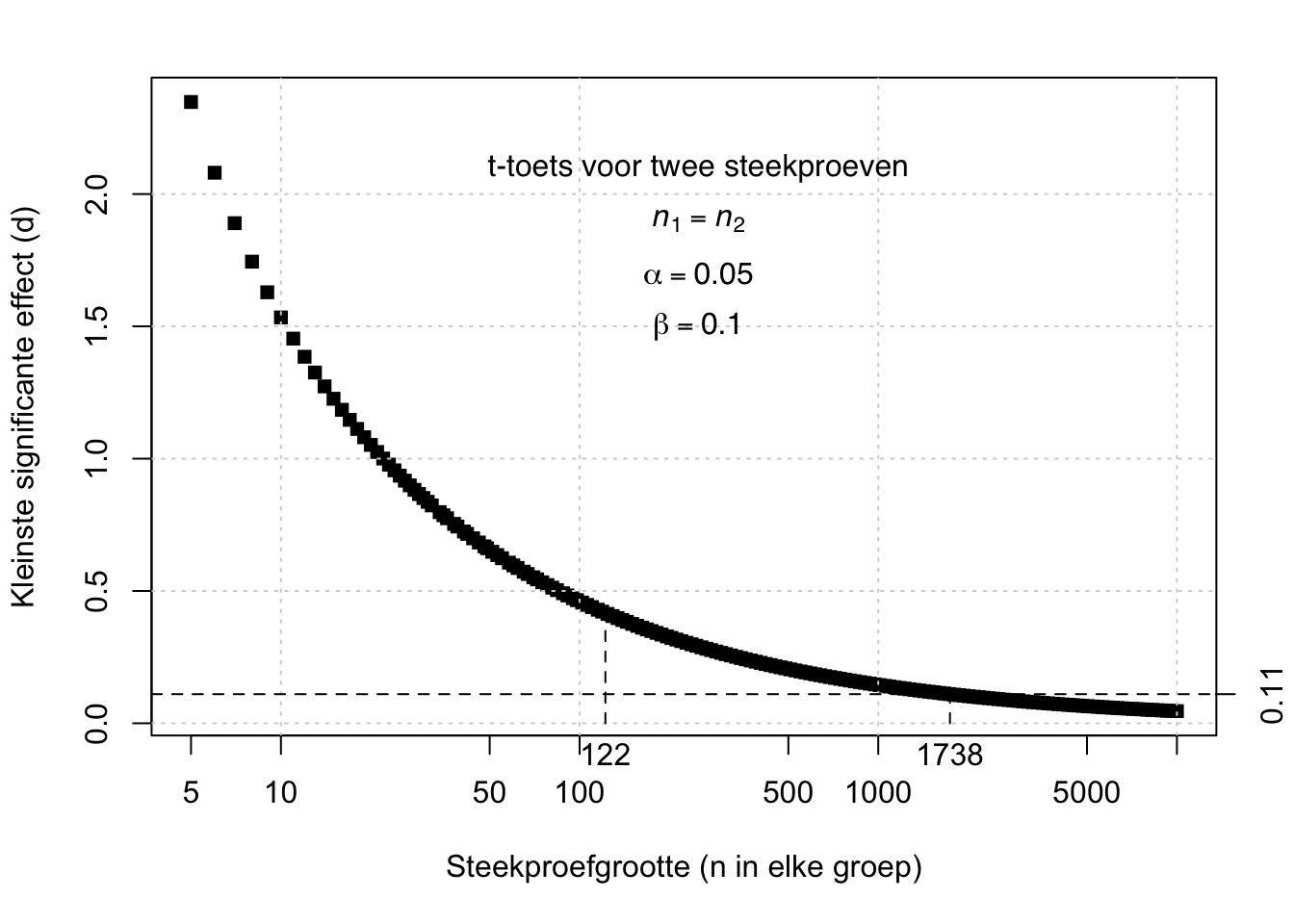
Relatie tussen de steekproefgrootte en het kleinste effect (d) dat significant is volgens een *t*-toets voor ongepaarde, onafhankelijke waarnemingen, met foutkansen alpha=.05 en beta=.10.

Figuur 13.3: Relatie tussen de steekproefgrootte en het kleinste effect (d) dat significant is volgens een t-toets voor ongepaarde, onafhankelijke waarnemingen, met foutkansen alpha=.05 en beta=.10.

Voorbeeld 13.3: Kijk nog eens naar formule (13.9) en naar Figuur 13.3 die de relatie tussen steekproefgrootte en effectgrootte illustreert. Met een steekproefgrootte van \(n_1=122\) kunnen we alleen een effect van \(d=0.42\) of groter opsporen, met voldoende kleine kansen op fouten van Typen I en II (\(\alpha=.05, \beta=.10\)). Om het zeer kleine effect van \(d=0.11\) op te sporen, met dezelfde kleine foutkansen \(\alpha\) en \(\beta\), zouden er steekproeven van tenminste 1738 meisjes en 1738 jongens nodig zijn.

We kunnen de effectgrootte ook uitdrukken als de waarschijnlijkheid dat een verschil in de voorspelde richting optreedt, voor een willekeurig gekozen element uit de populatie (formules (13.11) en (13.13)), of (indien van toepassing) voor twee willekeurig en onafhankelijk gekozen elementen uit de twee populaties (formule (13.12)) (McGraw and Wong 1992). Laten we nog eens terugkeren naar de grammaticatoets van de studenten Taalwetenschap (§13.2). Het effect dat we vonden is niet alleen significant maar ook groot. In termen van waarschijnlijkheid uitgedrukt: de kans dat een willekeurige student Taalwetenschap een score behaalt groter dan \(\mu_0=73\) is 0.91. (En een willekeurig gekozen student Taalwetenschap heeft dus nog 9% kans om lager te scoren dan het veronderstelde populatie-gemiddelde van 73.)

Voor de fictieve oordelen over de webpagina’s met U of je (zie Tabel 13.1) vinden we een gestandaardiseerde effectgrootte van \[d = \frac{ \overline{D}-\mu_D} {s_D} = \frac{ -2.20-0 } {1.03} = -2.13\] Dat dit extreem grote effect inderdaad significant is, wekt dan ook geen verbazing. We kunnen dat als volgt rapporteren:

De oordelen van \(N=10\) respondenten over de pagina’s met U of je als aanspreekvorm verschillen significant, met gemiddeld \(-2.2\) punten verschil. Dit verschil heeft een 95% betrouwbaarheidsinterval van \(-2.9\) tot \(-1.5\) en een geschatte gestandaardiseerde effectgrootte \(d=-2.13\); de kans dat een willekeurig gekozen respondent de je-versie hoger beoordeelt dan de U-versie is \(p=.98\).

13.8.1 formules

Voor een enkele steekproef: \[\begin{equation} \tag{13.11} d = \frac{\overline{x}-\mu}{s} \end{equation}\] waarbij \(s\) de standaarddeviatie \(s\) van de score \(x\) voorstelt.

Voor twee onafhankelijke steekproeven (zie formule (13.3)): \[\begin{equation} \tag{13.12} d = \frac{ \overline{x_1}-\overline{x_2} } { s_p } \end{equation}\]

Voor gepaarde waarnemingen: \[\begin{equation} \tag{13.13} d = \frac{ \overline{x_1}-\overline{x_2} } { s_D } \end{equation}\] waarbij \(s_D\) de standaarddeviatie is van het verschil \(D\) volgens formule (13.13).

13.8.2 SPSS

In SPSS kunnen we de effectgrootte meestal het makkelijkste met de hand uitrekenen.

Voor een enkele steekproef (formule (13.11)) kunnen we de effectgrootte eenvoudig uitrekenen uit het gemiddelde en de standaarddeviatie, rekening houdend met de waarde \(\mu\) waartegen we toetsen.

Analyze > Descriptive Statistics > Descriptives...

Kies de knop Options en zorg dat Mean en Std.deviation zijn aangevinkt. In de uitvoer staan vervolgens de benodigde gegevens:
\(d = (84.41 - 73) / 8.392 = 1.36\), een zeer groot effect.

Voor ongepaarde, onafhankelijke waarnemingen kunnen we eveneens de effectgrootte het beste met de hand uitrekenen op basis van de gemiddelden, standaarddeviaties, en omvang van de twee steekproeven, gebruik makend van formules (13.3) en (13.12) hierboven.

Voor een enkele steekproef met twee gepaarde observaties (formule (13.13)) kunnen we de effectgrootte weer eenvoudiger uitrekenen uit het gemiddelde en de standaarddeviatie van het verschil. De gegevens staan in de uitvoer van de paarsgewijze \(t\)-toets (§13.7.3), respectievelijk als Mean en Std.Deviation:
\(d = -2.200 / 1.033 = 2.130\), een super groot effect.

13.8.3 JASP

In JASP kan de effectgrootte worden opgevraagd bij het doen van een \(t\)-toets, door simpelweg Effect size aan te vinken onder “Additional Statistics”. Zie hiervoor de JASP instructies voor een \(t\)-toets voor een enkele steekproef (§13.2.5), een \(t\)-toets voor twee onafhankelijke groepen (§13.6.4) en een \(t\)-toets voor gepaarde waarnemingen (§13.7.4).
De uitvoer van de \(t\)-toets zal (Cohen’s) d aangeven: de effectgrootte. Onder Effect size kan ook Confidence interval worden aangevinkt (dit staat standaard op 95%, maar kan ook worden veranderd) voor het betrouwbaarheidsinterval van de effectgrootte (zie §13.8.5 hieronder).

13.8.4 R

In R is het wat makkelijker om de effectgrootte te laten uitrekenen.

Voor een enkele steekproef (formule (13.11)):

gramm2013 <- read.csv( file="data/grammaticatoets2013.csv",header=F)
dimnames(gramm2013)[[2]] <- c("score","opleiding")
with(gramm2013, score[opleiding=="TW"]) -> score.TW # hulpvariabele
( mean(score.TW)-73 ) / sd(score.TW) 
## Warning in mean.default(score.TW): argument is not numeric or logical:
## returning NA
## [1] NA

De kans op een score groter dan het populatiegemiddelde (de toetswaarde) 73 voor een willekeurige student Taalwetenschap (waarvan we aannemen dat \(\mu=84.4\) en \(s=8.4\)):

1 - pnorm( 73, mean=84.4, sd=8.4 ) 
## [1] 0.9126321

Voor ongepaarde, onafhankelijke waarnemingen kunnen we het kleinste significante effect uitrekenen (zie ook Fig. 13.3); daarvoor gebruiken we de functie power.t.test. (Deze functie is ook gebruikt om Fig.13.3 te construeren.) Je moet bij die functie de gewenste power als argument opgeven (power = \(1-\beta\); zie §14.1).

power.t.test( n=122, sig=.05, power=.90, type="two.sample" )
## 
##      Two-sample t test power calculation 
## 
##               n = 122
##           delta = 0.4166921
##              sd = 1
##       sig.level = 0.05
##           power = 0.9
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

In de uitvoer staat bij delta het kleinste significante effect aangegeven; zie ook Voorbeeld 13.3 hierboven.

Voor een enkele steekproef met twee gepaarde observaties (formule (13.13)):

ujedata <- read.table( file="data/ujedata.csv", header=TRUE, sep=";" )
with( ujedata, mean(cond.u-cond.je) / sd(cond.u-cond.je) )
## [1] -2.130141

13.8.5 Betrouwbaarheidsinterval van de effectgrootte

We hebben al eerder gezien (§10.7 en §13.5) dat we een kenmerk of parameter van de populatie kunnen schatten op basis van een kenmerk van een steekproef. Zo hebben we het onbekende populatiegemiddelde \(\mu\) geschat op basis van het geobserveerde steekproefgemiddelde \(\overline{x}\). Bij die schatting hoort wel een bepaalde mate van onzekerheid of betrouwbaarheid: misschien verschilt de onbekende parameter in de populatie enigszins van het steekproefkenmerk, dat we als schatter gebruiken, ten gevolge van toevallige variaties in de steekproef. De (on)zekerheid of (on)betrouwbaarheid wordt uitgedrukt als een betrouwbaarheidsinterval van het geschatte kenmerk. Als we herhaalde steekproeven uit de populatie zouden (kunnen) trekken, dan ligt het onbekende gemiddelde van de populatie binnen het betrouwbaarheidsinterval van de steekproef, in 95% van de herhaalde steekproeven (zie §10.7 en §13.5).

Deze redenatie nu geldt niet alleen voor de gemiddelde score, of voor de mediaan of voor de variantie, maar evenzo voor de effectgrootte. Ook de effectgrootte is immers een onbekende parameter uit de populatie, die we proberen te schatten op grond van een beperkte steekproef. Voor de fictieve oordelen over de webpagina’s met U of je (zie Tabel 13.1) vonden we een gestandaardiseerde effectgrootte van \(d=-2.13\). Dit is een schatting van de onbekende effectgrootte (d.i. van de sterkte van de voorkeur voor de je-variant) in de populatie van beoordelaars, op basis van een steekproef van \(n=10\) beoordelaars. We kunnen ook hier de betrouwbaarheid van deze schatting aangeven, in de vorm van een betrouwbaarheidsinterval rondom de geobserveerde effectgrootte \(d=-2.13\).

Het betrouwbaarheidsinterval van de effectgrootte is wel wat lastig vast te stellen (Nakagawa and Cuthill 2007; Chen and Peng 2015). We illustreren het hier op simpele wijze voor het simpelste geval, nl. dat van de \(t\)-toets voor een enkele steekproef, c.q. voor twee gepaarde observaties. We hebben hiervoor twee elementen nodig: ten eerste de effectgrootte uitgedrukt als correlatie (Rosenthal and Rosnow 2008, 359, formule 12.1), \[r = \sqrt{ \frac{t^2}{t^2+\textrm{df}} }\] en ten tweede de standaardfout van de effectgrootte \(d\) (Nakagawa and Cuthill 2007, 600, formule 18): \[\begin{equation} \tag{13.14} \textrm{se}_d = \sqrt{ \frac{2(1-r)}{n} + \frac{d^2}{2(n-1)} } \end{equation}\] In ons eerdere voorbeeld van de \(n=10\) gepaarde oordelen over een webpagina met U of je als aanspreekvorm vonden we \(d=-2.13\). We vinden ook dat \(r=.91\). Met deze gegevens vinden we \(\textrm{se}_d = 0.52\) via formule (13.14).

Hiermee bepalen we vervolgens het betrouwbaarheidsinterval voor de effectgrootte: \[\begin{equation} \tag{13.15} d \pm t^*_{n-1} \times \textrm{se}_d \end{equation}\] (zie de overeenkomstige formule (13.2)). Na invullen van \(t^*_9=2.262\) (zie Bijlage C) en \(\textrm{se}_d = 0.519\) vinden we uiteindelijk een 95%-betrouwbaarheidsinterval van \((-3.30,-0.96)\). Met 95% betrouwbaarheid ligt de onbekende effectgrootte in de populatie binnen dit interval (als we herhaalde steekproeven zouden trekken uit de populatie, dan zou in 95% van de herhaalde steekproeven de onbekende ware effectgrootte in de populatie binnen het gevonden betrouwbaarheidsinterval voor de effectgrootte vallen). Aangezien het betrouwbaarheidsinterval geheel kleiner is dan nul (negatief), mogen we concluderen dat de ware effectgrootte waarschijnlijk negatief is. Op grond van die laatste overweging kunnen we H0 verwerpen. En: we weten nu niet alleen dat de voorkeur afwijkt van nul, maar ook in welke mate de (gestandaardiseerde) voorkeur afwijkt van nul, d.w.z. hoe sterk de voorkeur voor de je-versie is. Deze nieuwe kennis over de mate of grootte van het effect is vaak nuttiger en interessanter dan de binaire beslissing of er wel of niet een effect is (H0 wel of niet verwerpen) (Cumming 2012).

Referenties

Alderson, Phil. 2004. “Absence of Evidence Is Not Evidence of Absence: We Need to Report Uncertain Results and Do It Clearly.” British Medical Journal 328 (7438): 476–77. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC351831/.
Andersson, Ida, Jenny Gaudin, Anna Graca, Katarina Holm, Linda Öhlin, Ulrika Marklund, and Anna Ericsson. 2011. “Productive Vocabulary Size Development in Children Aged 18-24 Months: Gender Differences.” KTH Speech, Music and Hearing: Quarterly Progress and Status Report 51 (1). http://www.speech.kth.se/prod/publications/files/3605.pdf.
Chen, Li-Ting, and Chao-Ying Joanne Peng. 2015. “The Sensitivity of Three Methods to Nonnormality and Unequal Variances in Interval Estimation of Effect Sizes.” Behavior Research Methods 47 (1): 107–26.
Cohen, Jacob. 1988. Statistical Power Analysis for the Behavioral Sciences. 2e ed. Hillsdale, N.J.: Lawrence Erlbaum.
Cumming, Geoff. 2012. Understanding the New Statistics. New York: Routledge.
Doblhammer, Gabriele. 1999. “Longevity and Month of Birth: Evidence from Austria and Denmark.” Demographic Research 1 (3). http://www.demographic-research.org/Volumes/Vol1/3.
McGraw, Kenneth O., and S. P. Wong. 1992. “A Common Language Effect Size Statistic.” Psychological Bulletin 111 (2): 361–65.
Nakagawa, Shinichi, and Innes C. Cuthill. 2007. “Effect Size, Confidence Interval and Statistical Significance: A Practical Guide for Biologists.” Biological Reviews 82 (4): 591–605. http://dx.doi.org/10.1111/j.1469-185X.2007.00027.x.
Rosenthal, Robert, and Ralph L. Rosnow. 2008. Essentials of Behavioral Research: Methods and Data Analysis. 3e ed. Boston: McGraw Hill.
Sagan, Carl. 1996. The Demon-Haunted World: Science as a Candle in the Dark. Random House.
Sawilowsky, Shlomo. 2009. “New Effect Size Rules of Thumb.” Journal of Modern Applied Statistical Methods 8 (2). https://doi.org/10.22237/jmasm/1257035100.
Thompson, Bruce. 2002. “‘Statistical,’ ‘Practical,’ and ‘Clinical’: How Many Kinds of Significance Do Counselors Need to Consider?” Journal of Counseling and Development 80 (1): 64–71.
Wright, Daniel B. 2003. “Making Friends with Your Data: Improving How Statistics Are Conducted and Reported.” British Journal of Educational Psychology 73 (1): 123–36. https://doi.org/10.1348/000709903762869950.

  1. Wij danken Els Rose voor het beschikbaar stellen van deze gegevens.↩︎

  2. In dit geval gebruiken we \(s_p = \sqrt{ \frac{122\times82^2+128\times98^2} {122+128} } = 90.5\), zie formules (13.3) en (13.12).↩︎