Hoofdstuk 14 Power
14.1 Inleiding
Bij statistische toetsing van H0 bepalen we de kans \(P\) op de geobserveerde verschillen of effecten (of op nog grotere verschillen of effecten dan geobserveerd) indien H0 waar zou zijn, en dus indien het geobserveerde verschil louter aan het toeval toegeschreven moet worden (zie §2.5 en Hoofdstuk 13). Als die kans \(P\) zeer klein is, dan hebben we dus resultaten gevonden die zeer onwaarschijnlijk zijn als H0 waar zou zijn. We concluderen dan dat H0 vermoedelijk niet waar is en we verwerpen daarom H0. Het gevonden verschil of effect noemen we dan “significant” (Latijn: ‘betekenis makend’). Er is echter wel een kans, \(P\), dat het gevonden verschil toch een toevalstreffer was, en dat we door H0 te verwerpen een fout van Type-I maken (d.w.z. H0 ten onrechte verwerpen, zie §13.1). Omdat we een bepaald significantieniveau \(\alpha\) hanteren waarmee we \(P\) vergelijken, is deze \(\alpha\) dus ook de kans dat we een Type-I-fout maken.
Minstens even belangrijk, echter, is de omgekeerde fout om H0 ten onrechte niet te verwerpen, een Type-II-fout. Voorbeelden van deze fouten zijn: een verdachte niet veroordelen ook al is hij schuldig, een ‘spam’ mail-bericht doorlaten naar mijn mailbox, een patiënt onderzoeken en diens ziekte toch niet opmerken, concluderen dat vogels zwijgen hoewel ze toch zingen (voorbeeld 13.1), of ten onrechte concluderen dat twee groepen niet verschillen hoewel er wel een belangrijk verschil bestaat tussen de twee groepen. De kans op een Type-II-fout wordt aangeduid met het symbool \(\beta\).
Als H0 in werkelijkheid niet waar is (er is een verschil, het bericht is ‘spam’, de vogels zingen, enz), dan dient H0 dus verworpen te worden, en dient \(\beta\) dus zo klein mogelijk te zijn. De kans om H0 dan terecht te verwerpen is dan \((1-\beta)\) (zie complementregel (10.3)); deze kans \((1-\beta)\) wordt de power genoemd. Power is op te vatten als de kans voor de onderzoeker om gelijk te krijgen (H0 wordt verworpen) als zij ook gelijk heeft (H0 is onwaar).
De kansen op fouten van Type-I en Type-II moeten goed tegen elkaar afgewogen worden. In veel onderzoek worden als overschrijdingskansen gehanteerd \(\alpha=.05\) (significantieniveau) en \(\beta=.20\) (power=\(.80\)). Hiermee wordt een impliciete afweging gemaakt dat een Type-I-fout \(4\times\) zo ernstig is als een Type-II-fout. Voor sommige onderzoeken zou dat gerechtvaardigd kunnen zijn, maar het is ook goed denkbaar dat onder bepaalde omstandigheden een Type-II-fout eigenlijk nog ernstiger is dan een Type-I-fout. Als we beide typen fouten min of meer even ernstig vinden, dan zouden we dus moeten streven naar een kleinere \(\beta\) en grotere power (Rosenthal and Rosnow 2008).
De power van een onderzoek hangt af van drie factoren: (i) de effectgrootte \(d\), die zelf weer afhankelijk is van het gemeten verschil \(D\) en van de variatie \(s\) in de observaties (formule (13.10)), (ii) de steekproefgrootte \(N\), en (iii) het significantieniveau \(\alpha\). In de volgende paragrafen zullen we deze factoren afzonderlijk bespreken, waarbij we de andere twee factoren zoveel mogelijk constant houden. Bij deze bespreking gebruiken we afbeeldingen van de berekende power (Figuren 14.1 en 14.2). De afgebeelde power-contouren zijn specifiek voor een t-toets voor onafhankelijke steekproeven (§13.6) met tweezijdige toetsing. De hieronder besproken verbanden treden echter ook op bij andere statistische toetsen.
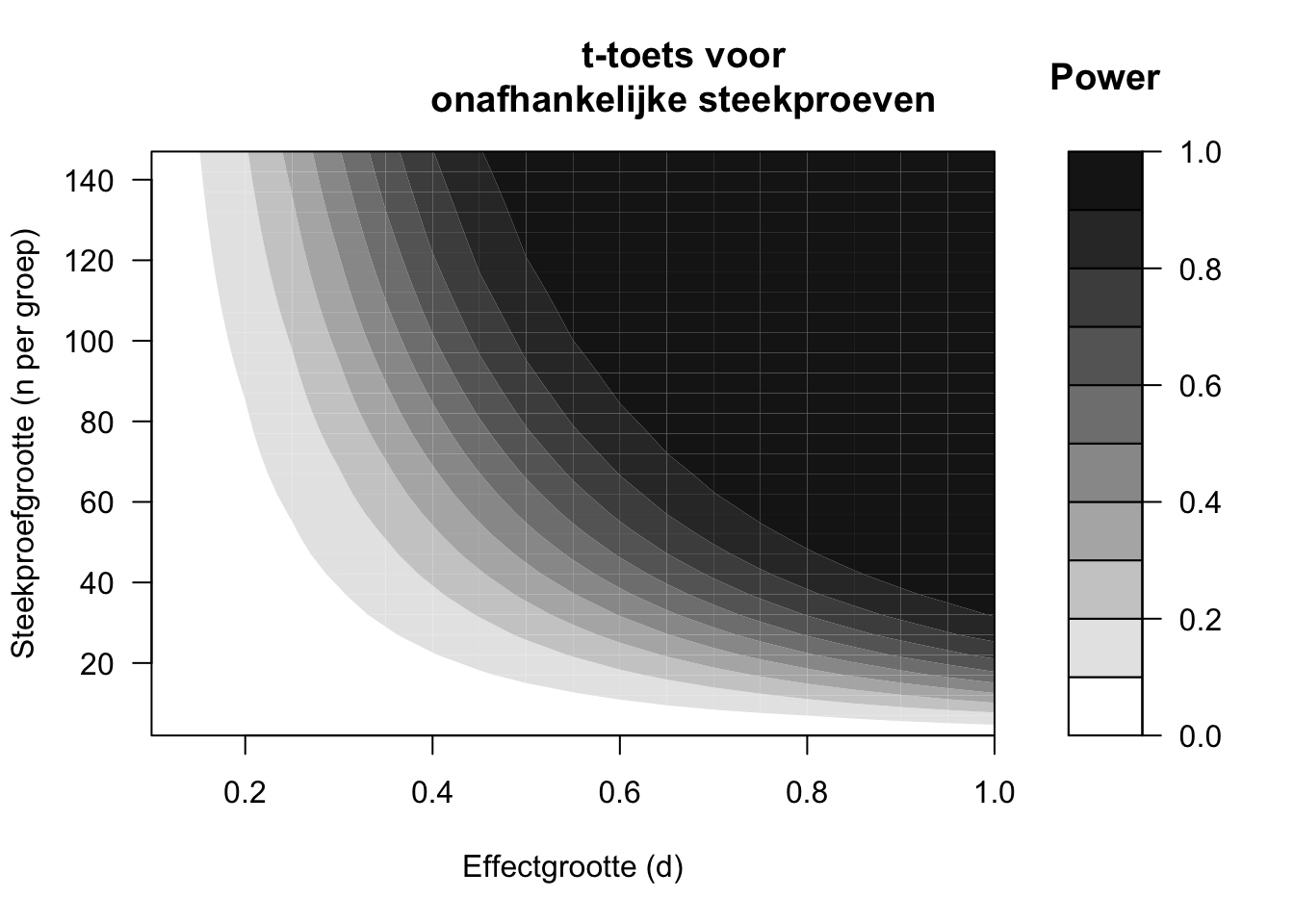
Figuur 14.1: Power uitgedrukt in contouren (zie schaalverdeling), afhankelijk van de gestandaardiseerde effectgrootte (d) en de steekproefgrootte (n), volgens een tweezijdige t-toets voor ongepaarde, onafhankelijke waarnemingen, met significantieniveau alpha=.01.
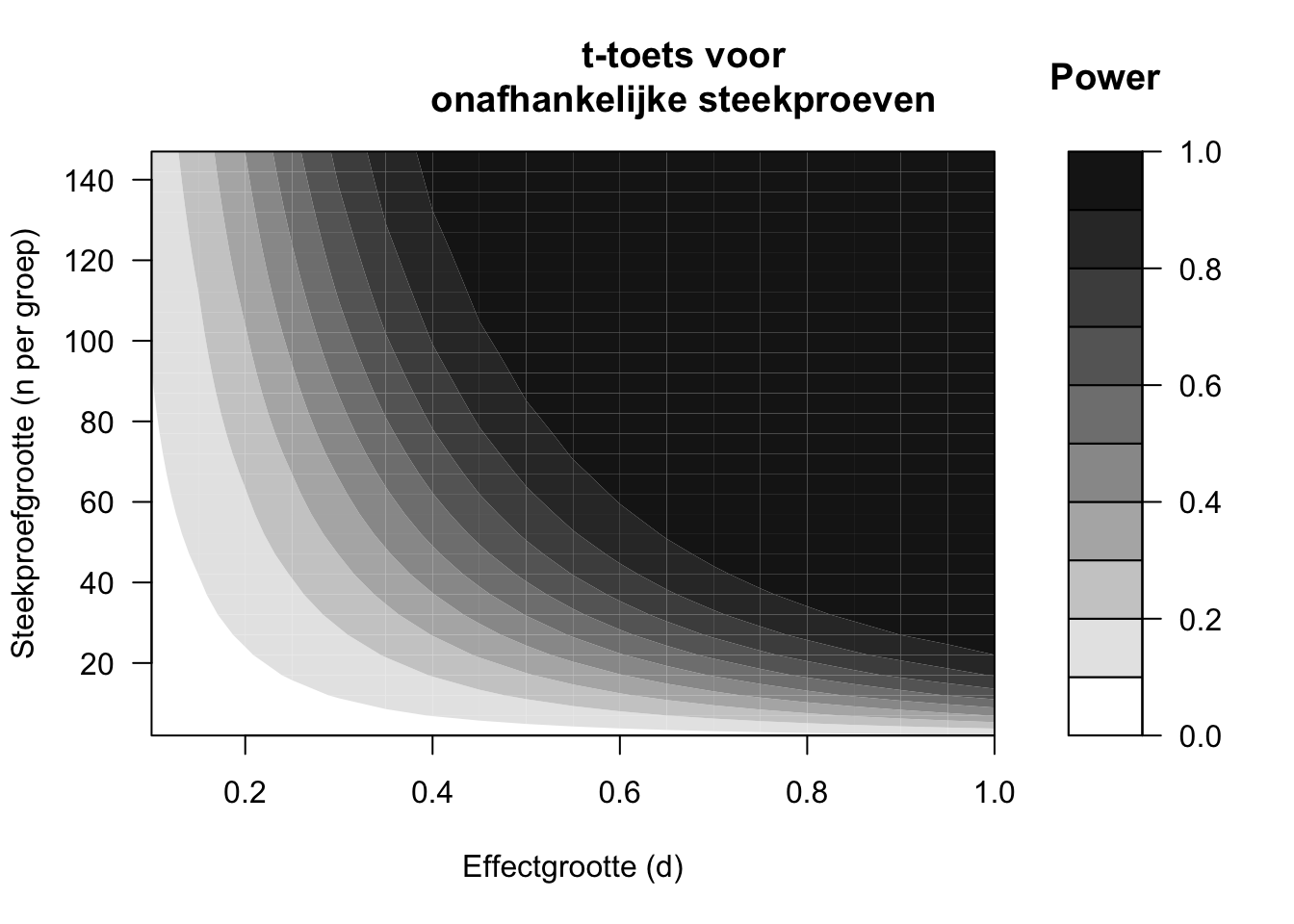
Figuur 14.2: Power uitgedrukt in contouren (zie schaalverdeling), afhankelijk van de gestandaardiseerde effectgrootte (d) en de steekproefgrootte (n), volgens een tweezijdige t-toets voor ongepaarde, onafhankelijke waarnemingen, met significantieniveau alpha=.05.
14.2 Verband tussen effectgrootte en power
De twee figuren 14.1 en 14.2 laten zien dat in het algemeen de power toeneemt, naarmate het te toetsen effect groter is (meer naar rechts in elke figuur). Dat is ook niet verwonderlijk: een groter effect heeft een grotere kans om opgespoord te worden in een statistische toets dan een kleiner effect, onder dezelfde omstandigheden. Een middelmatig groot effect van \(d=.5\) heeft, bij \(n=30\) observaties in elke groep, slechts een kans van \(.48\) om opgespoord te worden (als \(\alpha=.05\), Figuur 14.2). Op basis van een onderzoek met \(n=30\) observaties per groep is het dus eigenlijk een grote gok of een onderzoeker zo’n effect (met \(d=.5\)) wel zal opsporen, en H0 zal verwerpen. Anders gezegd, de kans op een Type-I-fout is weliswaar veilig laag (\(\alpha=.05\)) maar de kans op een Type-II-fout is meer dan \(10\times\) zo groot, en daarmee gevaarlijk hoog (\(\beta=.52\)) (Rosenthal and Rosnow 2008, Ch.12).
Een groter effect heeft een grotere kans om opgespoord te worden. Een groter effect van \(d=.8\), bijvoorbeeld, resulteert in een power van \(.86\) bij dezelfde toetsing. De kans op een Type-II-fout \(\beta=.14\) is weliswaar ook hier groter dan de kans op een Type-I-fout, maar de verhouding \(\beta/\alpha\) is aanzienlijk minder scheef.
Als onderzoeker hebben we alleen indirect invloed op de effectgrootte. We hebben uiteraard geen invloed op het ware ruwe verschil \(D\) in de populatie. Voor de power is echter niet dat ruwe verschil \(D\) van belang, maar het gestandaardiseerde verschil \(d=D/s\) (§13.8). Dus als we zorgen dat de standaarddeviatie \(s\) op enige wijze kleiner wordt, dan wordt daarmee \(d\) groter, en dan wordt daarmee weer de power groter (figuren 14.1 en 14.2), en dan hebben we dus meer kans om een bestaand effect daadwerkelijk op te sporen! Vanwege dat doel streven onderzoekers er altijd naar om storende invloeden van allerlei andere factoren zoveel mogelijk te neutraliseren. Die storende invloeden zorgen immers voor extra variabiliteit in de observaties, en daarmee voor een lagere power bij de statistische toetsing.
In een goed opgezet onderzoek willen we vooraf al bepalen wat de power zal zijn, en hoe groot de steekproef dient te zijn (zie hierna). Daarvoor hebben we een schatting nodig van de kleinste effectgrootte \(d\) die we nog willen opsporen (§13.8) (Quené 2010). Om de effectgrootte te schatten, is ten eerste een schatting nodig van het ruwe verschil \(D\) tussen de groepen of condities. Ten tweede is er een schatting nodig van de variabiliteit \(s\) in de observaties. Die schattingen zijn meestal af te leiden uit eerdere publicaties, waarin doorgaans ook de standaarddeviatie \(s\) wordt gerapporteerd. Als er geen eerdere onderzoeksrapporten beschikbaar zijn, dan kan \(s\) grofweg geschat worden uit enkele informele ‘pilot’-observaties. Neem daarvan het verschil tussen de hoogste en de laagste (bereik of ‘range’), deel dit bereik door 4, en gebruik de uitkomst daarvan als grove schatting voor \(s\) (Peck and Devore 2008).
14.3 Verband tussen steekproefgrootte en power
Het verband tussen de steekproefgrootte \(N\) en de power van een onderzoek wordt geïllustreerd in Figuur 14.1 voor een streng significantieniveau \(\alpha=.01\), en in Figuur 14.2 voor het meest gebruikte significantieniveau \(\alpha=.05\). De figuren laten zien dat in het algemeen de power toeneemt, naarmate de steekproef groter wordt (meer naar boven). De toename is steiler (power neemt sneller toe) bij grotere effecten (rechterkant) dan bij kleinere effecten (linkerkant). Anders gezegd: bij kleine effecten is de steekproef eigenlijk bijna altijd te klein om deze kleine effecten met voldoende power te kunnen opsporen. We zagen dat al eerder in voorbeeld 13.3 (Hoofdstuk 13).
De twee figuren 14.1 en 14.2 zijn gebaseerd op de vergelijking tussen twee groepen die even groot zijn, elk met precies de helft van de observaties (\(n_1=n_2=N/2\)). Dat is ook het meest efficiënt. De power is gebaseerd op het harmonisch gemiddelde van \(n_1\) en \(n_2\) (zie §9.3.4), en dat harmonisch gemiddelde is altijd kleiner dan het rekenkundig gemiddelde van die twee getallen. Het is dus raadzaam om ervoor te zorgen dat de groepen of steekproeven die je vergelijkt ongeveer even groot zijn.
Voorbeeld 14.1: In een studie worden twee groepen proefpersonen vergeleken, met \(n_1=10\) en \(n_2=50\) (\(N=n_1+n_2=10+50=60\)). Het harmonisch gemiddelde van \(n_1=10\) en \(n_2=50\) is \(H=17\). Deze studie heeft dus dezelfde power als een kleinere studie met twee groepen van elk 17 proefpersonen, dus 34 proefpersonen in totaal. Voor deze studie zijn er dus 26 proefpersonen méér onderzocht (en belast) dan noodzakelijk (zie ook §3.2) (Aron, Coups, and Aron 2011, 295).
14.4 Verband tussen significantieniveau en power
Het verband tussen het significantieniveau \(\alpha\) en de power wordt geïllustreerd door het verschil tussen de twee figuren 14.1 en 14.2. Voor iedere combinatie van effectgrootte en steekproefgrootte is de power lager in Figuur 14.1 voor \(\alpha=.01\) dan in Figuur 14.2 voor \(\alpha=.05\). Als we het significantieniveau \(\alpha\) hoger kiezen, dan neemt de kans toe om H0 te verwerpen, en dus ook de power om H0 terecht te verwerpen als H0 onwaar is (zie Tabel 2.2). Maar helaas neemt met een hoger significantieniveau \(\alpha\) ook de kans toe om H0 ten onrechte te verwerpen als H0 waar is (d.w.z. om een Type-I-fout te maken). De onderzoeker moet een afweging maken tussen fouten van Type-I (met kans \(\alpha\)) of van Type-II (met kans \(\beta\)); zoals eerder gezegd moet deze afweging afhangen van de ernst van (de consequenties van) deze twee typen van fouten.
14.5 Nadelen van onvoldoende power
Helaas zijn er zeer veel voorbeelden te vinden van ‘underpowered’ onderzoek in het domein van taal en communicatie. Dit onderzoek heeft een te kleine kans om H0 te verwerpen als het onderzochte effect wel bestaat (H0 is niet waar). Waarom is dat kwalijk (Quené 2010)?
Ten eerste kan de Type-II-fout die hier optreedt ernstige consequenties hebben: een behandelmethode die eigenlijk beter is, wordt niet als zodanig erkend, een patiënt wordt niet of onjuist gediagnostiseerd, een nuttige innovatie wordt ten onrechte terzijde geschoven. Deze fout belemmert de groei van onze kennis en ons inzicht, en belemmert de wetenschappelijke vooruitgang (zie ook voorbeeld 3.2 in Hoofdstuk 3).
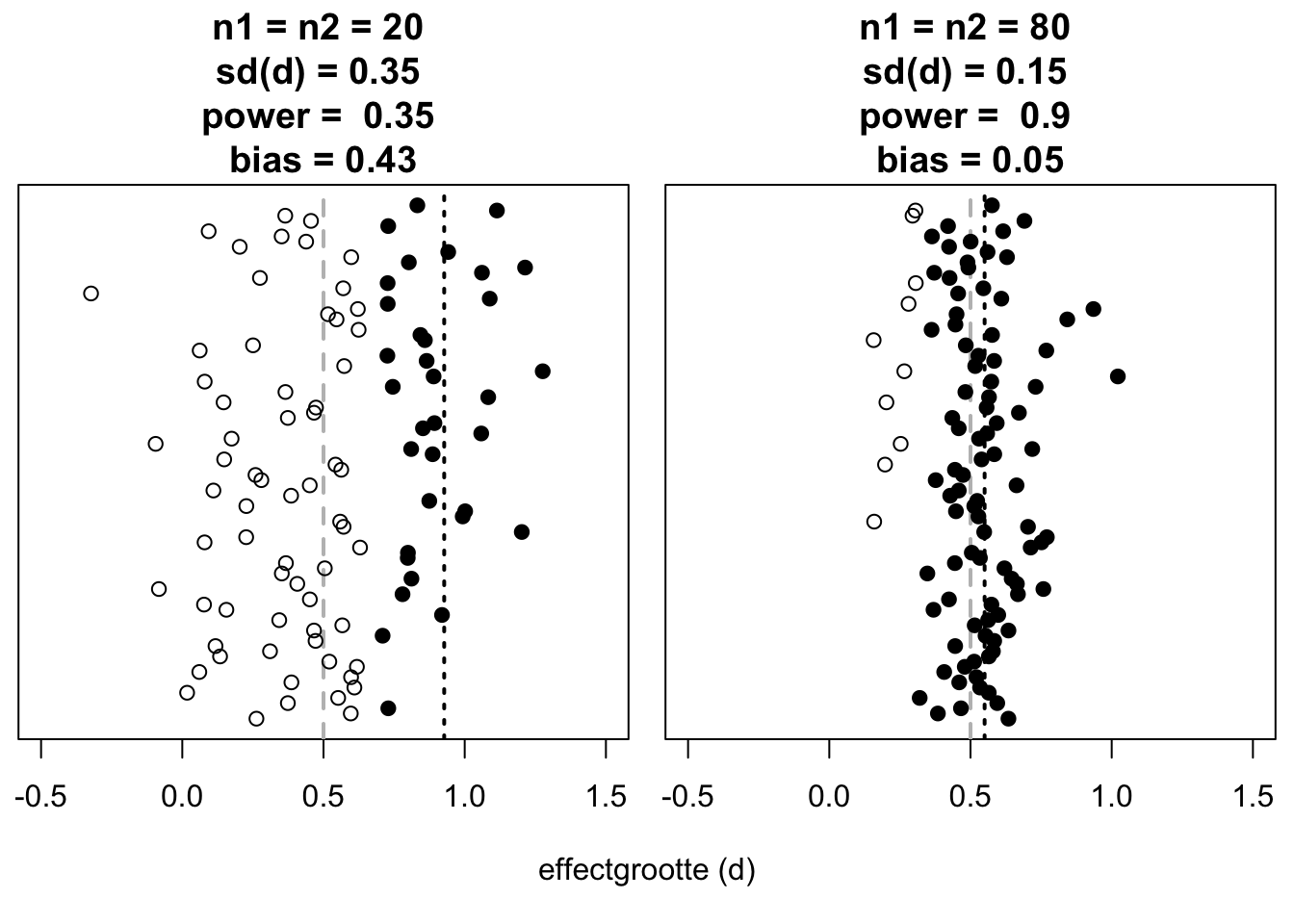
Figuur 14.3: Gevonden effectgroottes (langs horizontale as) in gesimuleerde experimenten (tweezijdige t-toets voor onafhankelijke waarnemingen, alpha=.05), uitgesplitst naar steekproefgrootte (links \(n=20\), rechts \(n=80\)) en naar toetsingsresultaat (donkere symbolen: wel significant; lichte symbolen: niet significant). De ware effectgrootte tussen groepen is altijd \(d=0.5\), aangegeven met grijze stippellijn. De gemiddelde gevonden effectgrootte van de significante uitkomsten is aangegeven met zwarte stippellijn. Voor iedere steekproefgrootte zijn 100 simulaties uitgevoerd (langs verticale as).
De uitkomsten van gesimuleerde experimenten met verschillende steekproefgrootte, en dus met verschillende power, zijn samengevat in Figuur 14.3. We leggen het tweede nadeel uit aan de hand van deze wat complexe figuur. In het linker paneel van Figuur 14.3 zien we dat de verschillende (simulaties van) ‘underpowered’ onderzoeken een gemengd beeld laten zien. Sommige van deze onderzoeken laten wèl een significant effect zien (donkere symbolen), en veel andere onderzoeken niet (lichte symbolen). Dat gemengde beeld leidt dan doorgaans tot vervolgonderzoek, waarin men probeert om uit te zoeken waarom het effect wel optrad in sommige onderzoeken, en niet in andere. Zou het verschil in resultaten toe te schrijven zijn aan verschillen in stimuli? proefpersonen? taken? instrumentatie? Al dat vervolg-onderzoek is echter overbodig: het gemengde beeld van deze onderzoeken is goed te verklaren door de geringe power van elk onderzoek. Het nodeloze en overbodige vervolg-onderzoek kost veel tijd en geld (en indirecte kosten, zie Hoofdstuk 3), en het gaat ten koste van ander, nuttiger onderzoek (Schmidt 1996, 118). Anders gezegd: één goed ontworpen studie met ruim voldoende power kan vele nodeloze vervolg-studies voorkomen.
Het derde nadeel is gebaseerd op de ervaring dat onderzoek waarin wèl een significant effect gevonden wordt (donkere symbolen), een grotere kans heeft om gerapporteerd te worden; dit verschijnsel wordt ‘publication bias’ of het ‘file drawer problem’ genoemd. Immers, een positief resultaat wordt vaak wel gepubliceerd en een negatief resultaat verdwijnt vaak in een bureaulade. Bij geringe power leidt dat tot een derde nadeel, nl. een overschatting of ‘bias’ van de gerapporteerde effectgrootte. In een underpowered studie, immers, moet een gevonden effect tamelijk groot zijn om gevonden te worden. In het meest linkse paneel zien we dat er slechts \(31\times\) een significant effect gevonden wordt. De gemiddelde effectgrootte van deze 31 significante uitkomsten is \(\overline{d_{\textrm{signif}}}=0.90\) (zwarte stippellijn), d.w.z. een vertekening of ‘bias’ van \(0.40\) ten opzichte van de eigenlijke \(d=0.50\) (grijze stippellijn)31. In het meest rechtse paneel zien we dat er \(91\times\) een significant effect gevonden wordt (dus de power is hier voldoende). De gemiddelde effectgrootte van deze 91 significante uitkomsten wijkt nauwelijks af van de eigenlijke \(d\). Bovendien is de standaarddeviatie van de gerapporteerde effectgrootten kleiner, en dat is weer van belang voor later onderzoek, meta-studies, en systematische reviews.
Ten vierde brengt het gemengde beeld van de verschillende onderzoeken, met soms wel en soms niet significante uitkomsten, en met grote variatie in de gerapporteerde effectgrootte, het gevaar met zich mee dat deze uitkomsten minder serieus genomen worden door ‘afnemers’ van wetenschappelijke kennis (behandelaars, zorgverzekeraars, ontwikkelaars, beleidsmakers, e.d.). Deze afnemers krijgen zo de indruk dat de wetenschappelijke evidentie voor dit onderzochte effect niet sterk is, en/of dat de onderzoekers het oneens zijn over of dat effect bestaat en zo ja hoe groot het dan is (Van Kolfschooten 1993) (Figuur 14.3). Ook dat belemmert de wetenschappelijke vooruitgang, en het belemmert het gebruik van wetenschappelijke inzichten in maatschappelijke toepassingen.
Om al deze bezwaren te vermijden moeten onderzoekers al in een vroeg stadium rekening houden met de gewenste power van een onderzoek. Het opzetten en uitvoeren van een onderzoek met onvoldoende power is immers in strijd met de eerder besproken ethische en morele principes van zorgvuldigheid en verantwoordelijkheid (§3.1).
Referenties
Een replicatie-studie die wel voldoende power heeft, vindt dus typisch een kleiner effect dan de originele ‘underpowered’ studie. Het kleinere effect gevonden in de replicatie-studie is dan typisch ook niet significant. We zeggen dan dat de replicatie-studie “fails to replicate” het effect dat in de originele studie wel significant was – maar dat eigenlijk een spurieuze vondst was.↩︎