Hoofdstuk 15 Variantieanalyse

15.1 Inleiding

Dit hoofdstuk gaat over een veel gebruikte statistische analyse, genaamd variantie-analyse (Eng. ‘analysis of variance’, vaak afgekort als ANOVA). In dit hoofdstuk gebruiken we relatief veel Engelse terminologie, ten eerste omdat de Nederlandse termen nauwelijks gebruikt worden, en daarmee samenhangend om goed aan te sluiten bij de Engelstalige vakliteratuur over variantieanalyse.

Hoe zit dit hoofdstuk in elkaar? We beginnen in paragraaf 15.2 met enkele voorbeelden van onderzoek waarvan de uitkomsten getoetst kunnen worden met variantieanalyse. De bedoeling van de paragraaf is je vertrouwd te maken met de techniek, met de nieuwe terminologie, en met de voorwaarden waaronder van deze techniek gebruik mag worden gemaakt. In §15.3.1 introduceren we de techniek op een intuïtieve wijze door in te gaan op de gedachtegang achter de toets. In §15.3.2 leiden we een formele vorm af voor de belangrijkste toetsingsgrootheid, de \(F\)-ratio.

15.2 Enkele voorbeelden

Variantieanalyse is, net als de t-toets, een statistische generalisatietechniek, dat wil zeggen: een instrument dat gebruikt kan worden bij de formulering van uitspraken over de eigenschappen van populaties, op basis van gegevens ontleend aan steekproeven uit die populaties. In het geval van de t-toets en van ANOVA gaan die uitspraken over het al dan niet gelijk zijn van de gemiddelden van (twee of meer) populaties. In deze zin kan variantieanalyse dan ook opgevat worden als een uitgebreide versie van de t-toets: met ANOVA kunnen we gegevens analyseren van meer dan twee steekproeven. Bovendien is het mogelijk om de effecten van meerdere onafhankelijke variabelen simultaan in de analyse te betrekken. Dat komt van pas als we gegevens willen analyseren uit een factorieel ontwerp (§6.8).

---

Voorbeeld 15.1: In dit voorbeeld onderzoeken we het spreektempo ofwel de spreeksnelheid van vier groepen sprekers, nl. afkomstig uit het Midden, Noorden, Zuiden en Westen van Nederland. De spreeksnelheid is uitgedrukt als de gemiddelde duur van een lettergreep, gemiddeld over een interview van ca 15 minuten met elke spreker (Quené 2008) (Quene 2022). Een kortere gemiddelde syllabeduur correspondeert dus met een snellere spreker (vgl. de schaatssport: een kortere rondetijd correspondeert met een snellere schaatser). Er waren 20 sprekers per groep, maar 1 spreker (uit het Zuiden) met een extreem hoge waarde is hier verwijderd uit de steekproef.

---

De geobserveerde spreeksnelheden per spreker uit bovenstaand voorbeeld 15.1 zijn samengevat in Tabel 15.1 en Figuur 15.1. Hierbij is de regio van herkomst een onafhankelijke categoriale variabele of ‘factor’. De waarden van deze factor worden ook aangeduid als ‘niveaus's’ (Eng. ‘levels’), of in veel onderzoeken als ‘groepen’ of ‘condities’. Ieder niveau of iedere groep of conditie vormt een ‘cel’ van het ontwerp, en de observaties uit die cel worden ook ‘replicaties’ genoemd (bedenk waarom die zo genoemd worden). De spreeksnelheid vormt de afhankelijke variabele. De nulhypothese luidt dat de gemiddelden van de afhankelijke variabele gelijk zijn voor alle groepen, dus H0: \(\mu_M = \mu_N = \mu_Z = \mu_W\). Als we H0 verwerpen, dan betekent dat dus alleen dat niet alle gemiddelden gelijk zijn, maar het betekent niet dat ieder groepsgemiddelde afwijkt van ieder ander groepsgemiddelde. Daarvoor is nader (post-hoc) onderzoek nodig; we komen daar later nog op terug.

Tabel 15.1: Gemiddelde spreeksnelheden, met standaarddeviatie en aantallen sprekers, verdeeld naar regio van herkomst van de spreker (zie voorbeeld 15.1).

regio	gemiddelde	s.d.	n
Midden	0.253	0.028	20
Noord	0.269	0.029	20
Zuid	0.260	0.030	19
West	0.235	0.028	20

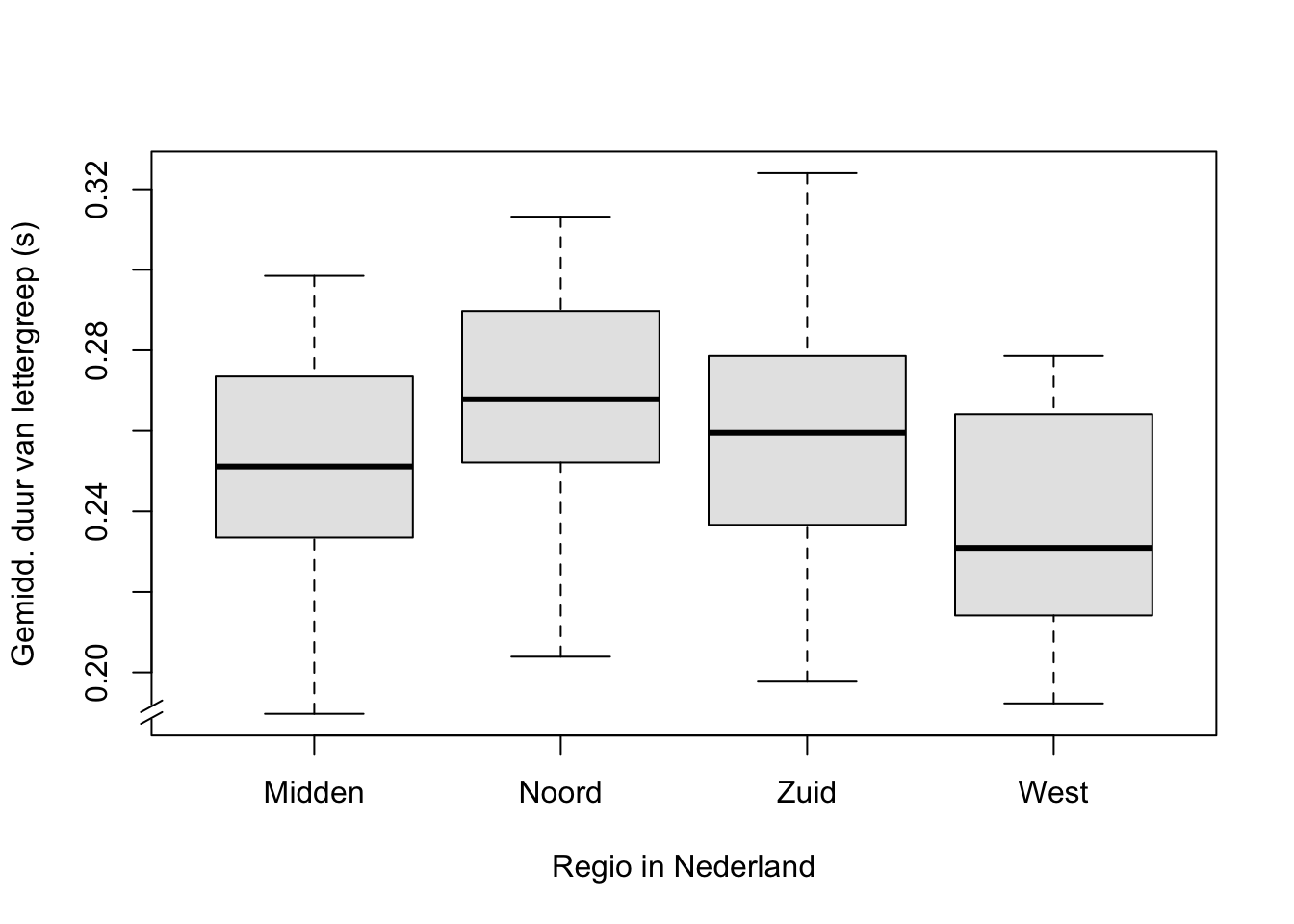
Figuur 15.1: Boxplot van de gemiddelde duur van de lettergrepen, opgesplitst naar regio van herkomst van de spreker.

Om nu te onderzoeken of de vier populaties verschillen in hun gemiddelde spreeksnelheid, zouden we in eerste instantie \(t\)-toetsen kunnen uitvoeren voor alle paren van niveaus. (Met 4 niveaus zou dat 6 toetsen vereisen, zie vergelijking (10.6) met \(n=4\) en \(x=2\)). Er kleven echter verschillende bezwaren aan deze aanpak. Eén daarvan bespreken we hier. Bij iedere \(t\)-toets gebruiken we een overschrijdingskans van \(\alpha=.05\). We hebben dus een kans van .95 op een juiste beslissing zonder Type-I-fout. De kans dat we bij alle 6 toetsen een juiste beslissing nemen is \(.95^6 = .73\) (volgens de productregel, vergelijking (10.4)). De gezamenlijke kans op één of meer Type-I-fout(en) in de 6 toetsen is dus niet meer \(.05\), maar is nu opgelopen tot \(1-.73 = .27\), ruim een kwart!

Variantieanalyse nu biedt de mogelijkheid om op grond van één enkele toetsing (dus niet 6 toetsen) de houdbaarheid te onderzoeken van de bovengenoemde nulhypothese. Variantieanalyse kan dus het beste gekenschetst worden als een globale toetsingstechniek, die het meest geschikt is als je a priori geen specifieke voorspellingen kan of wil doen omtrent de verschillen tussen de populaties.

Een variantieanalyse toegepast op de scores samengevat in Tabel 15.1 zal tot verwerping van de nul-hypothese leiden: de 4 regionale gemiddelden zijn niet gelijk. De gevonden verschillen zijn hoogstwaarschijnlijk niet toe te schrijven aan toevallige steekproeffluctuaties, maar aan systematische verschillen tussen de groepen (\(\alpha=.05\)). Kan nu geconcludeerd worden dat de gevonden verschillen in spreeksnelheid veroorzaakt worden door verschil in herkomst van de spreker? Hier is terughoudendheid geboden (zie §5.2). Het is immers niet uit te sluiten dat de vier populaties niet alleen in spreeksnelheid systematisch van elkaar verschillen, maar ook in andere relevante factoren, die niet in het onderzoek opgenomen zijn, zoals gezondheid, welvaart, of onderwijs. Die andere factoren zouden we alleen kunnen uitsluiten als we proefpersonen aselect zouden toewijzen aan de gekozen niveaus van de onafhankelijke variabele. Dat is echter niet mogelijk als het gaat om de regio van herkomst van de spreker: we kunnen een spreker meestal wel (aselect) toewijzen aan een behandelvorm of conditie, maar niet aan een regio van herkomst. In feite is het onderzoek in voorbeeld 15.1 dus quasi-experimenteel.

Voor ons tweede voorbeeld betrekken we een tweede factor in hetzelfde onderzoek naar spreeksnelheid, nl. ook het geslacht van de spreker. ANOVA stelt ons in staat om in één enkele analyse te toetsen of (i) de vier regio’s van elkaar verschillen (H0: \(\mu_M = \mu_N = \mu_Z = \mu_W\)), en of (ii) de twee geslachten van elkaar verschillen (H0: \(\mu_\textrm{vrouw} = \mu_\textrm{man}\)), en of (iii) de verschillen tussen de regio’s hetzelfde zijn voor beide geslachten (of, anders gezegd, of de verschillen tussen de geslachten hetzelfde zijn voor alle regio’s). Dat laatste noemen we de ‘interactie’ tussen de twee factoren.

Tabel 15.2: Gemiddelde spreeksnelheden, met standaarddeviatie en aantallen sprekers, verdeeld naar geslacht en regio van herkomst van de spreker (zie voorbeeld 15.1).

geslacht	regio	gemiddelde	s.d.	n
vrouw	Midden	0.271	0.021	10
vrouw	Noord	0.285	0.025	10
vrouw	Zuid	0.269	0.028	9
vrouw	West	0.238	0.028	10
man	Midden	0.235	0.022	10
man	Noord	0.253	0.025	10
man	Zuid	0.252	0.030	10
man	West	0.232	0.028	10

De resultaten in Tabel 15.2 suggereren dat (i) sprekers uit het Westen sneller spreken dan de anderen, en dat (ii) mannen sneller spreken dan vrouwen (!). En (iii) het verschil tussen mannen en vrouwen lijkt kleiner voor sprekers uit het Westen dan voor sprekers uit andere regionen. Uiteraard zouden we deze effecten moeten toetsen om de bovenstaande uitspraken te onderbouwen (zie daarvoor §15.4 hieronder).

15.2.1 aannames

De variantie-analyse vereist vier aannames (of assumpties) waaraan voldaan moet zijn, om deze toets te mogen gebruiken; deze aannames komen overeen met die van de t-toets (§13.2.3).

• De gegevens moeten gemeten zijn op intervalniveau (zie §4.4).

• Alle observaties moeten onafhankelijk van elkaar zijn.

• De scores moeten normaal verdeeld zijn binnen elke groep (zie §10.4).

• De variantie van de scores moet (ongeveer) gelijk zijn in de scores van de respectievelijke groepen of condities (zie §9.5.1). Schending van deze aanname is ernstiger naarmate de steekproeven meer in grootte verschillen. Het is daarom verstandig om te werken met even grote, en liefst niet te kleine steekproeven.

Samenvattend: variantieanalyse kan gebruikt worden om meerdere populatiegemiddelden te vergelijken, en om de effecten van meerdere factoren en combinaties van factoren (interacties) te bepalen. Variantieanalyse vereist wel dat de gegevens aan meerdere voorwaarden voldoen.

15.3 Eén-weg-variantieanalyse

15.3.1 Een intuïtieve uitleg

Zoals gezegd gebruiken we variantieanalyse om te onderzoeken of de scores van verschillende groepen, of verzameld onder verschillende condities, van elkaar verschillen. Maar — scores verschillen altijd van elkaar, door toevallige fluctuaties tussen de replicaties binnen elke steekproef. In de voorgaande hoofdstukken zijn we al vele voorbeelden tegengekomen van toevalsfluctuaties binnen dezelfde steekproef en binnen dezelfde conditie. De vraag wordt dan, of de scores tussen de verschillende groepen (of verzameld onder verschillende condities) méér van elkaar verschillen dan je zou verwachten op grond van toevallige fluctuaties binnen elke groep of cel.

De bovengenoemde “verschillen tussen scores” vormen bij elkaar de variantie van die scores (§9.5.1). Bij variantieanalyse verdelen we de totale variantie in twee delen: ten eerste de variantie veroorzaakt door (systematische) verschillen tussen groepen, en ten tweede de variantie veroorzaakt door (toevallige) verschillen binnen groepen. Als H0 waar is, en als er dus (in de populaties) géén verschillen tussen de groepen zijn, dan verwachten we desalniettemin (in de steekproeven van de groepen) wèl enige verschillen tussen de gemiddelde scores van de groepen, zij het dat de laatstgenoemde verschillen niet groter zullen zijn dan de toevallige verschillen binnen de groepen, als H0 waar is. Lees deze alinea nog eens aandachtig door.

Deze aanpak wordt geïllustreerd in Figuur 15.2, waarin de scores zijn afgebeeld uit drie experimentele groepen (met aselecte toewijzing van proefpersonen aan de groepen): de rode, grijze en blauwe groep. De scores verschillen van elkaar, in ieder geval door toevallige fluctuaties van de scores binnen elke groep. Er zijn misschien ook systematische verschillen tussen (de gemiddelde scores van) de drie groepen. Maar zijn deze systematische verschillen nu relatief groter dan de toevallige verschillen binnen groepen? Zo ja, dan verwerpen we H0.

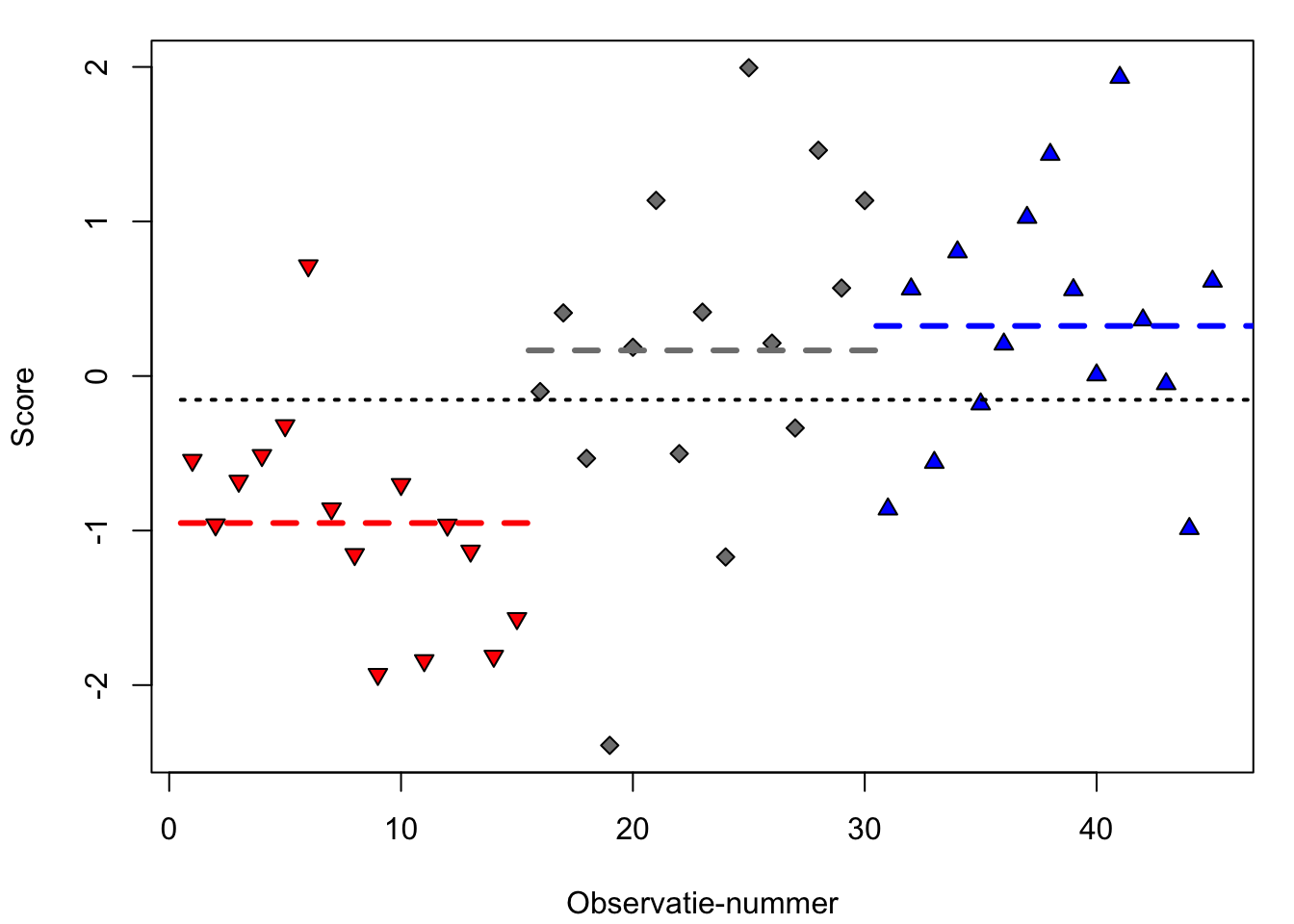
Figuur 15.2: Gesimuleerde observaties van drie experimentele groepen: rood (neerwaartse driehoek), grijs (ruit), en blauw (opwaartse driehoek) (n=15 per groep), met het gemiddelde per groep (in streeplijnen), en met het gemiddelde over alle observaties (stippellijn).

De systematische verschillen tussen de groepen corresponderen met de verschillen van de rode, grijze en blauwe groepsgemiddelden (streepjeslijnen in Figuur 15.2) ten opzichte van het gemiddelde over alle observaties (stippellijn). Voor de eerste observatie is dat een negatieve afwijking, want de score ligt onder het algemene gemiddelde (stippellijn). De toevallige verschillen binnen de groepen corresponderen met de afwijking van iedere observatie ten opzichte van het groepsgemiddelde (voor de eerste observatie is dat dus een positieve afwijking, want de score ligt boven het groepsgemiddelde van de rode groep).

Laten we nu de overstap maken van ‘verschillen’ naar ‘variantie’. We splitsen dan de afwijking van iedere observatie t.o.v. het algemene gemiddelde op in twee afwijkingen: ten eerste de afwijking van groepsgemiddelde t.o.v. algemene gemiddelde, en ten tweede de afwijking van iedere replicatie t.o.v. het groepsgemiddelde. Dat zijn twee stukjes variantie, die tezamen de totale variantie vormen. Omgekeerd kunnen we dus de totale variantie opdelen in deze twee componenten, vandaar de naam ‘variantieanalyse’. (We zullen in de volgende paragraaf uitleggen hoe die componenten berekend worden, rekening houdend met het aantal observaties en aantal groepen.)

Die verdeling van de totale variantie in twee variantiecomponenten is nuttig, omdat we daarna de verhouding of ratio tussen die twee delen kunnen bepalen. Die verhouding tussen varianties wordt de \(F\)-ratio genoemd, en we gebruiken deze verhouding om H0 te toetsen.

\[\textrm{H0}: \textrm{variantie tussen groepen} = \textrm{variantie binnen groepen}\]

\[\textrm{H0}: F = \frac{\textrm{variantie tussen groepen}}{\textrm{variantie binnen groepen}} = 1\]

De \(F\)-ratio is dus een toetsingsgrootheid, waarvan de kansverdeling bekend is indien H0 waar is. In het voorbeeld van Figuur 15.2 vinden we \(F=3.22\), met 3 groepen en 45 observaties, \(p<.001\). We vinden hier dus een relatief grote systematische variantie tussen groepen, ten opzichte van de relatief kleine toevallige variantie binnen groepen: de eerstgenoemde variantie (teller van verhouding \(F\)) is meer dan \(3\times\) zo groot als de laatstgenoemde variantie (noemer van verhouding \(F\)). De kans \(p\) om deze verhouding te vinden als H0 waar is, is buitengewoon gering, en we verwerpen daarom H0. (We zullen in de volgende paragraaf uitleggen hoe die kans bepaald wordt, weer rekening houdend met het aantal observaties en aantal groepen.) We spreken dan van een significant effect van de factor op de afhankelijke variabele.

Aan het slot van deze paragraaf herhalen we de essentie van de variantieanalyse. We verdelen de totale variantie in twee delen: de mogelijk systematische variantie tussen groepen of condities, en de variantie binnen groepen of condities (d.i. altijd aanwezige, toevallige fluctuatie tussen replicaties). De toetsingsgrootheid \(F\) bestaat uit de verhouding tussen deze twee varianties. We toetsen eenzijdig of \(F=1\), en verwerpen H0 als \(F>1\) zodanig dat de kans \(P(F|\textrm{H0}) < \alpha\). De gemiddelde scores van de groepen of condities zijn dan hoogstwaarschijnlijk niet alle gelijk. We weten daarmee nog niet welke groepen van elkaar verschillen, daarvoor is nog verdere (post-hoc) analyse nodig (§15.3.5 hieronder).

15.3.2 Een formele uitleg

Voor onze uitleg beginnen we met de geobserveerde scores. We nemen aan dat de scores zijn opgebouwd volgens een bepaald statistisch model, nl. als de optelsom van het populatiegemiddelde (\(\mu\)), een systematisch effect (\(\alpha_j\)) van de \(j\)’de conditie of groep (over \(k\) condities of groepen), en een toevallig effect (\(e_{ij}\)) voor de \(i\)’de replicatie binnen de \(j\)’de conditie of groep (over \(N\) replicaties in totaal). In formule: \[x_{ij} = \mu + \alpha_{j} + e_{ij}\] Ook hier weer ontleden we dus iedere score in een systematisch deel en een toevallig deel. Dat geldt niet alleen voor de scores zelf, maar ook voor de afwijkingen van iedere score ten opzichte van het totale gemiddelde (zie §15.3.1).

Er zijn derhalve drie varianties van belang. Ten eerste de totale variantie (zie vergelijking (9.3), afgekort tot t) over alle \(N\) observaties uit alle groepen of condities tezamen: \[\begin{equation} \tag{15.1} s^2_t = \frac{ \sum (x_{ij} - \overline{x})^2 } {N-1} \end{equation}\] Ten tweede de variantie tussen (Eng. ‘between’, afgekort totb) de groepen of condities: \[\begin{equation} \tag{15.2} s^2_b = \frac{ \sum_{j=1}^{j=k} n_j (\overline{x_j} - \overline{x})^2 } {k-1} \end{equation}\] en ten derde de variantie binnen (Eng. ‘within’, afgekort tot w) de groepen of condities: \[\begin{equation} \tag{15.3} s^2_w = \frac{ \sum_{j=1}^{j=k} \sum_i (x_{ij} - \overline{x_j})^2 } {N-k} \end{equation}\]

In deze vergelijkingen worden de tellers gevormd door de som van de gekwadrateerde afwijkingen (‘sums of squares’, afgekort SS). In de vorige paragraaf hebben we aangegeven dat de afwijkingen bij elkaar optellen, en dat geldt dan ook voor de gesommeerde en gekwadrateerde afwijkingen: \[\begin{align} \tag{15.4} { \sum (x_{ij} - \overline{x})^2 } &= { \sum_{j=1}^{j=k} n_j (\overline{x_j} - \overline{x})^2 } + { \sum_{j=1}^{j=k} \sum_i (x_{ij} - \overline{x_j})^2 } \\ \textrm{SS}_t &= \textrm{SS}_b + \textrm{SS}_w \end{align}\] De noemers van de varianties worden gevormd door de vrijheidsgraden (‘degrees of freedom’, afgekort df, zie §13.2.1). Voor de variantie tussen groepen \(s^2_b\) is dat het aantal groepen of condities, minus 1 (\(k-1\)). Voor de variantie binnen groepen \(s^2_w\) is dat het aantal observaties, minus het aantal groepen (\(N-k\)). Voor de totale variantie is dat het aantal observaties minus 1 (\(N-1\)). Ook de vrijheidsgraden van de afwijkingen tellen bij elkaar op: \[\begin{align} \tag{15.5} { (N-1) } &= { (k-1) } + { (N-k) } \\ \textrm{df}_t &= \textrm{df}_b + \textrm{df}_w \end{align}\]

De bovenstaande breuken die de varianties \(s^2_t\), \(s^2_b\) en \(s^2_w\) beschrijven, worden ook aangeduid als de ‘mean squares’ (afgekort MS). \(\textrm{MS}_{t}\) is per definitie gelijk aan de ‘gewone’ variantie \(s^2_x\) (zie de identieke vergelijkingen (9.3) en (15.1)).

De toetsingsgrootheid \(F\) is gedefinieerd als de verhouding van de twee hierboven gedefinieerde variantiecomponenten: \[\begin{equation} \tag{15.6} F = \frac{ s^2_b } { s^2_w } \end{equation}\] met niet één maar twee vrijheidsgraden, resp. \((k-1)\) voor de teller en \((N-k)\) voor de noemer.

De overschrijdingskans \(p\) die behoort bij de gevonden \(F\) kan je bepalen aan de hand van een tabel, maar meestal voeren we een variantieanalyse uit met behulp van de computer, en die berekent dan ook die overschrijdingskans.

De resultaten van een variantieanalyse worden samengevat met een vaste opbouw in een zgn. ANOVA-tabel, zoals Tabel 15.3. Daarin staat de belangrijkste informatie samengevat. Maar de hele tabel kan ook in één zin samengevat worden, zie Voorbeeld 15.2.

Tabel 15.3: Samenvatting van variantieanalyse van de observaties in Figuur 15.2.

variantiebron	df	SS	MS	\(F\)	\(p\)
groep	2	14.50	7.248	9.36	<.001
(within)	42	32.54	0.775

---

Voorbeeld 15.2: De gemiddelde scores zijn niet gelijk voor de rode, grijze en blauwe groep [\(F(2,42) = 9.35, p<.001, \omega^2 = .28\)].

---

15.3.3 Effectgrootte

Net als bij de \(t\)-toets is het niet alleen van belang om een binaire beslissing te nemen over H0, maar is het minstens zo belangrijk om te weten hoe groot het geobserveerde effect is (zie ook §13.8). Deze effectgrootte bij variantieanalyse kan worden uitgedrukt in verschillende maten, waarvan wij er twee bespreken (deze paragraaf is gebaseerd op Kerlinger and Lee (2000); zie ook Olejnik and Algina (2003)).

De eenvoudigste maat is de zgn. \(\eta^2\) (“èta-kwadraat” of “eta squared”), de proportie van de totale SS die toe te schrijven is aan de verschillen tussen de groepen of condities: \[\label{eq:etasq} \eta^2 = \frac{ \textrm{SS}_b } { \textrm{SS}_t }\] De effectgrootte \(\eta^2\) is een proportie tussen 0 en 1, die aangeeft hoeveel van de variantie in de steekproef toe te schrijven is aan de onafhankelijke variabele.

De tweede maat voor effectgrootte bij variantieanalyse is de zgn. \(\omega^2\) (“omega-kwadraat” of “omega squared”): \[\begin{equation} \tag{15.7} \omega^2 = \frac{ \textrm{SS}_b - (k-1) \textrm{MS}_w} { \textrm{SS}_t + \textrm{MS}_w } \end{equation}\] De effectgrootte \(\omega^2\) is ook een proportie; dit is een schatting van de proportie van de variantie in de populatie die toe te schrijven is aan de onafhankelijke variabele, waarbij de schatting uiteraard gebaseerd is op de onderzochte steekproef. Omdat we in het algemeen meer geïnteresseerd zijn in generalisatie naar de populatie dan naar de steekproef, geven wij de voorkeur aan \(\omega^2\) als maat voor de effectgrootte.

We dienen niet alleen de \(F\)-ratio, vrijheidsgraden, en overschrijdingskans te rapporteren, maar ook de effectgrootte (zie voorbeeld 15.2 hierboven).

“It is not enough to report \(F\)-ratios and whether they are statistically significant. We must know how strong relations are. After all, with large enough \(N\)s, \(F\)- and \(t\)-ratios can almost always be statistically significant. While often sobering in their effect, especially when they are low, coefficients of association of independent and dependent variables [i.e., effect size coefficients] are indispensable parts of research results” (Kerlinger and Lee 2000, 327, nadruk toegevoegd).

15.3.4 Gerichte vergelijkingen

In voorbeeld 15.2 (zie Figuur 15.2) onderzochten we de verschillen tussen scores uit de rode, zwarte en blauwe groepen. De nulhypothese die getoetst werd was H0: \(\mu_\textrm{rood} = \mu_\textrm{grijs} = \mu_\textrm{blauw}\). Het is echter ook goed mogelijk dat een onderzoeker al bepaalde ideeën heeft over de verschillen tussen de groepen, en gericht op zoek is naar bepaalde verschillen, en andere verschillen juist wil negeren. De gerichte vergelijkingen (Eng. ‘planned comparisons’) worden ook wel ‘contrasten’ genoemd.

Laten we voor hetzelfde voorbeeld aannemen dat de onderzoeker al verwacht, uit eerder onderzoek, dat de scores van de rode en blauwe groepen van elkaar zullen verschillen. De bovenstaande H0 is dan niet meer interessant om te onderzoeken, omdat we bij voorbaat verwachten H0 te zullen verwerpen. De onderzoeker wil nu gericht weten (1) of de rode groep lager scoort dan de andere twee groepen, (H0: \(\mu_\textrm{rood} = (\mu_\textrm{grijs}+\mu_\textrm{blauw})/2\)), en (2) of de grijze en blauwe groepen van elkaar verschillen (H0: \(\mu_\textrm{grijs} = \mu_\textrm{blauw}\)) ³².

De factor ‘groep’ of ‘kleur’ heeft 2 vrijheidsgraden, en dat betekent dat we precies 2 van zulke gerichte vergelijkingen of ‘contrasten’ kunnen maken die onafhankelijk zijn van elkaar. Dergelijke onafhankelijke contrasten worden ‘orthogonaal’ genoemd.

In een variantieanalyse met gerichte vergelijkingen wordt de variantie tussen groepen of condities nog verder opgedeeld, nl. in de gerichte contrasten zoals de twee hierboven (zie Tabel 15.4). We laten een verdere uitleg over gerichte vergelijkingen hier achterwege, maar adviseren wel om waar mogelijk slim gebruik te maken van deze gerichte vergelijkingen, indien je een meer specifieke nulhypothese kunt opstellen dan H0: “de gemiddelde scores zijn gelijk in alle groepen of condities”. We kunnen zo gerichte uitspraken doen over de verschillen tussen de groepen in ons voorbeeld:

---

Voorbeeld 15.3: De gemiddelde score van de rode groep is significant lager dan van de beide andere groepen gecombineerd [\(F(1,42)=18.47, p<.001, \omega^2=.28\)]. De gemiddelde score is nagenoeg gelijk voor de grijze en blauwe groep [\(F(1,42)<1, \textrm{n.s.}, \omega^2=.00\)]. Dit impliceert dat de rode groep significant lagere scores behaalt dan de grijze groep en dan de blauwe groep.

---

Tabel 15.4: Samenvatting van variantieanalyse van de observaties in Figuur 15.2, met gerichte contrasten tussen groepen.

variantiebron	df	SS	MS	\(F\)	\(p\)
groep	2	14.50	7.248	9.36	<.001
groep, contrast 1	1	14.31	14.308	18.47	<.001
groep, contrast 2	1	0.19	0.188	0.24	.62
(within)	42	32.54	0.775

De variantie-analyse met gerichte vergelijkingen is dus vooral bruikbaar als je, voordat de observaties zijn gedaan, al gerichte hypotheses hebt over verschillen tussen bepaalde (combinaties van) groepen of condities. Die hypotheses kunnen gebaseerd zijn op theoretische overwegingen, of op eerdere onderzoeksresultaten.

15.3.4.1 Orthogonale contrasten

Elk contrast kan worden uitgedrukt in de vorm van gewichten voor iedere conditie. Voor de hierboven besproken contrasten kan dat in de vorm van deze gewichten:

conditie	contrast 1	contrast 2
rood	-1	0
grijs	+0.5	-1
blauw	+0.5	+1

De H0 voor contrast 2 (\(\mu_\textrm{grijs} = \mu_\textrm{blauw}\)) is uit te drukken in gewichten als volgt: \(\textrm{C2} = 0\times \mu_\textrm{rood} -1 \times \mu_\textrm{grijs} +1 \times \mu_\textrm{blauw} = 0\).

Om te bepalen of twee contrasten orthogonaal zijn, vermenigvuldigen we hun respectievelijke gewichten voor iedere conditie (rij):
\(( (-1)(0), (+0.5)(-1), (+0.5)(+1) )= (0, -0.5, +0.5)\).
Vervolgens tellen we al deze producten bij elkaar op: \(0 -0.5 + 0.5 = 0\). Als de som van deze producten nul is, dan zijn de twee contrasten orthogonaal.

15.3.5 Post-hoc vergelijkingen

In veel onderzoeken heeft een onderzoeker géén idee over de te verwachten verschillen tussen de groepen of condities. Pas na afloop van de variantieanalyse, nadat er een significant effect gevonden is, besluit de onderzoeker om nader te inspecteren welke condities van elkaar verschillen. We spreken dan van post-hoc vergelijkingen, “suggested by the data” (Maxwell and Delaney 2004, 200). We moeten daarbij conservatief te werk gaan, juist omdat we na de variantieanalyse al kunnen vermoeden dat sommige vergelijkingen een significant resultaat zullen opleveren, d.w.z., de nulhypotheses zijn al niet neutraal.

Er zijn vele tientallen statistische toetsen voor post-hoc vergelijkingen. Het belangrijkste verschil is hun mate van conservatisme (neiging om H0 niet te verwerpen) vs. liberalisme (neiging om H0 wel te verwerpen). Daarnaast zijn sommige toetsen meer ingericht op paarsgewijze vergelijkingen tussen condities (‘pairwise comparisons’, zoals contrast 2 hierboven) en andere meer op complexe vergelijkingen (zoals contrast 1 hierboven). En de toetsen verschillen in de aannames die ze doen over de varianties in de cellen. We noemen hier één toets voor post-hoc-vergelijkingen tussen paren van condities: Tukey’s Honestly Significant Difference, afgekort Tukey’s HSD. Deze toets neemt een goede middenpositie in tussen te conservatief of te liberaal. Een belangrijke eigenschap van de Tukey HSD toets is dat de gezamenlijke overschrijdingskans (Eng. ‘family-wise error’) over alle paarsgewijze vergelijkingen tezamen gelijk is aan de opgegeven overschrijdingskans \(\alpha\) (zie §15.2). De Tukey HSD toets resulteert in een 95% betrouwbaarheidsinterval van het verschil tussen twee condities, en/of in een \(p\)-waarde van het verschil tussen twee condities.

---

Voorbeeld 15.4: De gemiddelde scores zijn niet gelijk voor de rode, grijze en blauwe groep [\(F(2,42) = 9.35, p <.001, \omega^2 = .28\)]. Post-hoc vergelijkingen met Tukey’s HSD-toets laten zien dat de grijze en blauwe groep niet van elkaar verschillen (\(p=.88\)), maar dat er wel significante verschillen zijn tussen de rode en de blauwe groep (\(p<.001\)) en tussen de rode en de grijze groep (\(p=.003\)).

---

15.3.6 SPSS

15.3.6.1 voorbereiding

We gebruiken de gegevens in het bestand data/kleurgroepen.txt; deze gegevens zijn ook weergegeven in Figuur 15.2. Lees eerst de benodigde gegevens, en controleer deze:

File > Import Data > Text Data...

Selecteer Files of type: Text en selecteer bestand data/kleurgroepen.txt. Bevestig met Open.
Namen van variabelen staan op regel 1. Decimale symbool is punt (period). Data beginnen op regel 2. Elke regel is een observatie. De gebruikte scheiding (delimiter) tussen variabelen is een spatie. Tekst staat tussen dubbele aanhalingstekens. De variabelen hoef je niet verder te definiëren, de standaardopties van SPSS werken hier goed.
Bevestig het laatste keuzescherm met Done. De gegevens worden dan ingelezen.

Onderzoek of de responsies normaal verdeeld zijn binnen elke groep, met behulp van de technieken uit Deel II van dit tekstboek (met name §10.4).

We kunnen in SPSS niet vooraf toetsen of de varianties gelijk zijn in de drie groepen, zoals vereist voor variantieanalyse. We doen dat tegelijk met de variantieanalyse zelf.

15.3.6.2 ANOVA

In SPSS kan je een variantieanalyse op meerdere manieren uitvoeren. We gebruiken hier een algemeen bruikbare aanpak, waarbij we aangeven dat er één afhankelijke variabele in het spel is.

Analyze > General Linear Model > Univariate...

Selecteer score als afhankelijke variabele (sleep naar paneel “Dependent variable”).
Selecteer kleur als onafhankelijke variabele (sleep naar paneel “Fixed Factor(s)”).
Kies Model... en daarna Full factorial model, Type I Sum of squares, en vink aan: Include intercept in model, en bevestig met Continue.
Kies Options... en vraag om gemiddelden voor de condities van de factor kleur (sleep naar paneel “Display Means for”). Vink aan: Estimates of effect size en Homogeneity tests, en bevestig weer met Continue.
Bevestig alle keuzes met OK.

In de uitvoer vinden we eerst de uitslag van Levene’s toets op gelijke varianties (homogeniteit van variantie), die geen aanleiding geeft om H0 te verwerpen. We mogen dus een variantieanalyse uitvoeren.

Daarna wordt de variantieanalyse samengevat in een tabel gelijkend op Tabel 15.3, waarbij ook de effectgrootte vermeld wordt in de vorm van  Partial eta square. Het is echter beter om \(\omega^2\) te rapporteren, maar je moet die dan wel zelf uitrekenen!

15.3.6.3 gerichte vergelijking

Voor een variantieanalyse met gerichte vergelijkingen moeten we de gewenste contrasten aangeven voor de factor kleur. De werkwijze is echter anders dan hierboven. We kunnen de gerichte contrasten in SPSS niet opgeven via het menu-systeem dat we tot nu toe gebruikten. We moeten hiervoor “onder de motorkap” gaan werken!
Herhaal daartoe eerst de instructies hierboven. Maar, in plaats van alles te bevestigen, kies je nu de knop Paste. Er wordt dan een zgn. Syntax-venster geopend (of geactiveerd, als het al open was). Je ziet daarin het SPSS-commando dat je via het menu hebt opgebouwd. We gaan dit commando bewerken om onze eigen, speciale contrasten aan te geven. Bij het specificeren van de contrasten moeten we wel rekening houden met de alfabetische ordening van de condities: blauw, grijs, rood.
Het commando in het Syntax-venster moet er uiteindelijk uitzien als hieronder, nadat je de regel /CONTRAST hebt toegevoegd. Het commando moet worden afgesloten met een punt.

UNIANOVA score BY kleur
  /METHOD=SSTYPE(1)
  /INTERCEPT=INCLUDE
  /EMMEANS=TABLES(kleur) 
  /PRINT=ETASQ HOMOGENEITY
  /CRITERIA=ALPHA(.05)
  /DESIGN=kleur
  /CONTRAST(kleur)=special(0.5 0.5 -1, 1 -1 0).

Plaats de cursor ergens tussen het woord UNIANOVA en de afsluitende punt, en klik dan op de grote groene pijl naar rechts (Run Selection) in het menu van het Syntax-venster.

De uitvoer geeft voor ieder contrast de significantie en het betrouwbaarheidsinterval van het getoetste contrast. Het eerste contrast is wel significant (Sig. .000, rapporteer als \(p<.001\), zie §13.3), en het tweede niet, zie Tabel 15.4.

15.3.6.4 post-hoc vergelijking

Herhaal eerst de instructies hierboven.
Kies de knop Post Hoc..., en selecteer de factor kleur (verplaats naar venster “Post Hoc Tests for:”). Vink aan: Tukey, en daarna Continue. Bevestig alle keuzes met OK.

Voor iedere paarsgewijze vergelijking zien we het verschil, de standaardfout, en de ondergrens (Lower Bound) en bovengrens (Upper Bound) van het 95% betrouwbaarheidsinterval van dat verschil. Als dat interval niet nul omvat, dan is het verschil tussen de twee groepen of condities dus waarschijnlijk niet gelijk aan nul. De gecorrigeerde overschrijdingskans volgens Tukey’s HSD toets is bovendien gegeven in de derde kolom. We zien dat rood verschilt van blauw, dat rood verschilt van grijs, en dat de scores van de grijze en blauwe groepen niet verschillen.

15.3.7 JASP

15.3.7.1 voorbereiding

We gebruiken de gegevens in het bestand data/kleurgroepen.txt; deze gegevens zijn ook weergegeven in Figuur 15.2. Lees de data in en controleer deze.

Onderzoek of de responsies normaal verdeeld zijn binnen elke groep, met behulp van de technieken uit Deel II van dit tekstboek (met name §10.4). Let op: Dit kan in JASP ook tegelijk met de variantieanalyse zelf, zie hieronder.

Het toetsen of de varianties gelijk zijn in de drie groepen, zoals vereist voor variantieanalyse, doen we tegelijk met de variantieanalyse zelf, zie hieronder.

15.3.7.2 ANOVA

Klik in de bovenbalk op:

ANOVA > ANOVA (onder 'Classical)

Selecteer de variabele score en plaats deze in het veld “Dependent Variable”, en plaats variabele kleur in het veld “Fixed Factors”.
Zorg dat onder “Display” Estimates of effect size is aangevinkt, en kies hier tussen \(\omega^2\) en (partial) \(\eta^2\). In dit boek houden we \(\omega^2\) aan. Je kunt ook Descriptive statistics aanvinken om beschrijvende statistiek van de scores per groep te krijgen. Dit geeft inzicht in wat je aan het testen bent.

Open de balk “Assumption Checks” en vink Homogeneity tests aan. “Homogeneity corrections” mag op None blijven staan. Je kunt hier ook onderzoeken of de verdeling binnen iedere groep normaal is, dat is equivalent aan een normale verdeling van de residuen van de variantieanalyse. Dat inspecteer je door hier ook Q-Q plot of residuals aan te vinken; in de resulterende Q-Q-plot zouden de residuen ongeveer op een rechte lijn moeten liggen (zie §10.4).

In de uitvoer wordt de variantieanalyse samengevat in een tabel gelijkend op Tabel 15.3, waarbij ook de effectgrootte vermeld wordt in de vorm van \(\omega^2\) en/of (partial) \(\eta^2\).

In de uitvoer vind je onder Assumption Checks ook de uitslag van Levene’s toets op gelijke varianties (homogeniteit van variantie). Die geeft geen aanleiding om H0 te verwerpen; we mogen dus een variantieanalyse uitvoeren.

15.3.7.3 gerichte vergelijking

Voor een variantieanalyse met gerichte vergelijkingen moeten we de gewenste contrasten aangeven voor de factor kleur. De werkwijze is in het begin hetzelfde als hierboven, herhaal dus de instructies onder ANOVA.

Open vervolgens de balk “Contrasts”. In het veld “Factors” staat als het goed is de variabele kleur en hierachter “none”. Selecteer in plaats van deze “none” de optie “custom”. Onder het veld verschijnt nu een werkblad “Custom for kleur”. Vul hier de gewenste waarden voor de contrasten in zoals eerder beschreven (zie §15.3.4.1). Voor contrast 1 \(-1\) voor rood en \(0.5\) voor blauw en grijs. Klik hierna op Add contrast en vul bij contrast 2 \(0\) in voor rood, \(-1\) voor grijs en \(1\) voor blauw.

De uitvoer geeft voor ieder contrast (Comparison) de significantie. Let op! In de tekst hierboven (§15.3.4) werden de gerichte contrasten getoetst met behulp van de toetsingsgrootheid \(F\); JASP gebruikt daarvoor echter de \(t\)-toets (voor twee onafhankelijke steekproeven). De \(p\)-waarde is hetzelfde. Rapporteer de toetsing van deze contrasten met behulp van de \(t\)-toets en \(p\)-waarde in de uitvoer van JASP, net zoals je bij een \(t\)-toets doet.

15.3.7.4 post-hoc vergelijking

Voor een variantieanalyse met post-hoc vergelijkingen moeten we de gewenste vergelijkingen aanvragen. De werkwijze is in het begin hetzelfde als hierboven, herhaal dus de instructies onder ANOVA.

Open vervolgens de balk “Post Hoc Tests” en verplaats variabele kleur naar het veld rechts. Zorg dat onder “Type” Standard is aangevinkt en daaronder ook Effect size. Vink onder “Correction” Tukey aan, en onder “Display” ook Confidence intervals.

De uitvoer geeft nu onder Post Hoc Tests de resultaten. Voor iedere paarsgewijze vergelijking zien we het verschil, de standaardfout, en de ondergrens en bovengrens van het 95% betrouwbaarheidsinterval van dat verschil. Als dat interval niet nul omvat, dan is het verschil tussen de twee groepen of condities dus waarschijnlijk niet gelijk aan nul. Voor iedere paarsgewijze vergelijking rapporteert JASP een \(t\)-toets, met aangepaste d.f. volgens Tukey’s HSD-toets. De aangepaste overschrijdingskans volgens Tukey’s HSD toets wordt gegeven in de laatste kolom. We zien dat rood verschilt van blauw, dat rood verschilt van grijs, en dat de scores van de grijze en blauwe groepen niet verschillen. In je eigen rapportage moet je vermelden dat Tukey’s HSD-toets is gebruikt, en wat de overschrijdingskansen zijn van elke post-hoc vergelijking (zie Voorbeeld 15.4).

15.3.8 R

15.3.8.1 voorbereiding

Lees eerst de benodigde gegevens, en controleer deze:

# zelfde data als gebruikt in Fig.15.2
kleurgroepen <- read.table( "data/kleurgroepen.txt", 
                            header=TRUE, stringsAsFactors=TRUE )

Onderzoek of de responsies normaal verdeeld zijn binnen elke groep, met behulp van de technieken uit Deel II van dit tekstboek (met name §10.4).

Onderzoek of de varianties gelijk zijn in de drie groepen, zoals vereist voor variantieanalyse. De H0 die we daarbij toetsen luidt: \(s^2_\textrm{rood} = s^2_\textrm{grijs} = s^2_\textrm{blauw}\). We toetsen deze H0 met behulp van Bartlett’s toets.

bartlett.test( x=kleurgroepen$score, g=kleurgroepen$kleur )

## 
##  Bartlett test of homogeneity of variances
## 
## data:  kleurgroepen$score and kleurgroepen$kleur
## Bartlett's K-squared = 3.0941, df = 2, p-value = 0.2129

15.3.8.2 ANOVA

summary( aov( score~kleur, data=kleurgroepen) -> m01 ) # zie Tabel 15.3

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## kleur        2  14.50   7.248   9.356 0.000436 ***
## Residuals   42  32.54   0.775                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

15.3.8.3 effectgrootte

# eigen functie om omega2 te berekenen, zie vergelijking (15.7) in de hoofdtekst, 
# voor effect genaamd `term` in summary(`model`)
omegasq <- function ( model, term ) {   
     mtab <- anova(model)
     rterm <- dim(mtab)[1] # resid term
     return( (mtab[term,2]-mtab[term,1]*mtab[rterm,3]) / 
             (mtab[rterm,3]+sum(mtab[,2])) )
     }
omegasq( m01, "kleur" ) # roep functie aan met 2 argumenten

## [1] 0.2708136

15.3.8.4 gerichte vergelijking

Bij het specificeren van de contrasten moeten we rekening houden met de alfabetische ordening van de condities: blauw, grijs, rood.

# maak matrix van twee orthogonale contrasten (per kolom, niet per rij) 
conmat <- matrix( c(.5,.5,-1, +1,-1,0), byrow=F, nrow=3 )
dimnames(conmat)[[2]] <- c(".R.GB",".0G.B") # (1) R vs G+B, (2) G vs B 
contrasts(kleurgroepen$kleur) <- conmat # wijs contrasten toe aan factor
summary( aov( score~kleur, data=kleurgroepen) -> m02 ) # uitvoer is nodig voor omega2

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## kleur        2  14.50   7.248   9.356 0.000436 ***
## Residuals   42  32.54   0.775                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# zie https://blogs.uoregon.edu/rclub/2015/11/03/anova-contrasts-in-r/
summary.aov( m02, split=list(kleur=list(1,2)) )

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## kleur        2  14.50   7.248   9.356 0.000436 ***
##   kleur: C1  1  14.31  14.308  18.470 0.000100 ***
##   kleur: C2  1   0.19   0.188   0.243 0.624782    
## Residuals   42  32.54   0.775                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Als we gerichte vergelijkingen hebben (planned contrasts) dan is de eerder geconstrueerde functie omegasq niet bruikbaar (en evenmin de eerder gegeven formule). We moeten de \(\omega^2\) nu met de hand uitrekenen met gebruik van de uitvoer van de samenvatting van model m02:

(14.308-1*0.775)/(0.775+14.308+0.19+32.54) # 0.28

## [1] 0.2830402

(0.188-1*0.775)/(0.775+14.308+0.19+32.54) # afgerond 0.00

## [1] -0.012277

15.3.8.5 post-hoc vergelijkingen

TukeyHSD(m02)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = score ~ kleur, data = kleurgroepen)
## 
## $kleur
##                  diff        lwr        upr     p adj
## grey50-blue -0.158353 -0.9391681  0.6224622 0.8751603
## red-blue    -1.275352 -2.0561668 -0.4945365 0.0007950
## red-grey50  -1.116999 -1.8978139 -0.3361835 0.0033646

Voor iedere paarsgewijze vergelijking zien we het verschil, en de ondergrens (lwr) en bovengrens (upr) van het 95% betrouwbaarheidsinterval van dat verschil. Als dat interval niet nul omvat, dan is het verschil tussen de twee groepen of condities dus waarschijnlijk niet gelijk aan nul. De gecorrigeerde overschrijdingskans volgens Tukey’s HSD toets is bovendien gegeven in de laatste kolom. Wederom zien we dat rood verschilt van grijs, dat rood verschilt van blauw, en dat de scores van de grijze en blauwe groepen niet verschillen.

15.4 Tweeweg-variantieanalyse

In §15.2 hebben we al een voorbeeld gegeven van een onderzoek met twee factoren die in één variantieanalyse onderzocht worden. We kunnen op deze manier onderzoeken (i) of er een hoofdeffect is van de eerste factor (bijv. regio van herkomst van de spreker), (ii) of er een hoofdeffect is van de tweede factor (bijv. geslacht van de spreker), en (iii) of er een interactie-effect is. Zo’n interactie houdt in dat de verschillen tussen condities van de ene factor niet hetzelfde zijn voor de condities van de andere factor, of anders gezegd, dat de gemiddelde score van een cel afwijkt van de voorspelde waarde op grond van de twee hoofdeffecten.

15.4.1 Een intuïtieve uitleg

In veel studies zijn we geïnteresseerd in de gecombineerde effecten van twee of meer factoren, zoals in het onderstaande voorbeeld dat we gebruiken voor onze uitleg.

---

Voorbeeld 15.5: Scholieren en studenten moeten veel studieteksten lezen én begrijpen (zoals deze!). Vermoedelijk is een studietekst beter te begrijpen, als die voorzien is van markeringen van de tekststructuur: tussenkopjes, signaalwoorden (bijv. echter, omdat), en dergelijke. Van Dooren, Van den Bergh, and Evers-Vermeul (2012) onderzochten of studieteksten mét dergelijke structuurmarkeringen beter te begrijpen zijn dan alternatieve versies van dezelfde teksten, maar dan zonder structuurmarkeringen. De eerste factor is dus de aanwezigheid danwel afwezigheid van structuurmarkeringen in de te bestuderen teksten.

Ook verwachten de onderzoekers een effect van de leesvaardigheid van de proefpersonen. Zwakke lezers zullen een tekst minder goed begrijpen dan sterke lezers. De tweede factor is dus het “lezerstype”, hier verdeeld in de drie categorieën ‘zwak’, ‘gemiddeld’, of ‘sterk’.

Bovendien verwachten de onderzoekers dat zwakke lezers de structuurmarkeringen meer nodig hebben, en dus meer baat erbij hebben, dan sterke lezers; “sterke lezers zijn in staat studieteksten met begrip te lezen, ongeacht de aanwezigheid van structuurmarkeringen” (Van Dooren, Van den Bergh, and Evers-Vermeul 2012, 33). De onderzoekers verwachten dus een interactie of wisselwerking tussen de factoren: de verschillen tussen de tekstversies zijn anders voor de verschillende lezerstypen, of anders gezegd, de verschillen tussen de lezerstypen zijn anders voor de verschillende tekstversies.

De resultaten in Figuur 15.3 tonen de drie onderzochte effecten in de begripsscore, voor een van de onderzochte teksten. Ten eerste zijn de begripsscores beter (hoger) voor de versie met structuurmarkeringen (licht) dan voor de versie zonder markeringen (donker). Ten tweede worden de verschillen tussen de lezerstypen bevestigd: zwakke lezers behalen over het algemeen lagere begripsscores dan gemiddelde lezers, en sterke lezers behalen over het algemeen hogere begripsscores.

Maar het meest opvallende effect is de interactie: het effect van tekstmarkeringen is veel groter bij zwakke lezers dan bij sterke lezers, conform de voorspelling. Of anders gezegd, de verschillen tussen zwakke, gemiddelde en sterke lezers zijn groot in de tekstversie zonder structuurmarkeringen, maar klein of nihil in de tekstversie met structuurmarkeringen.

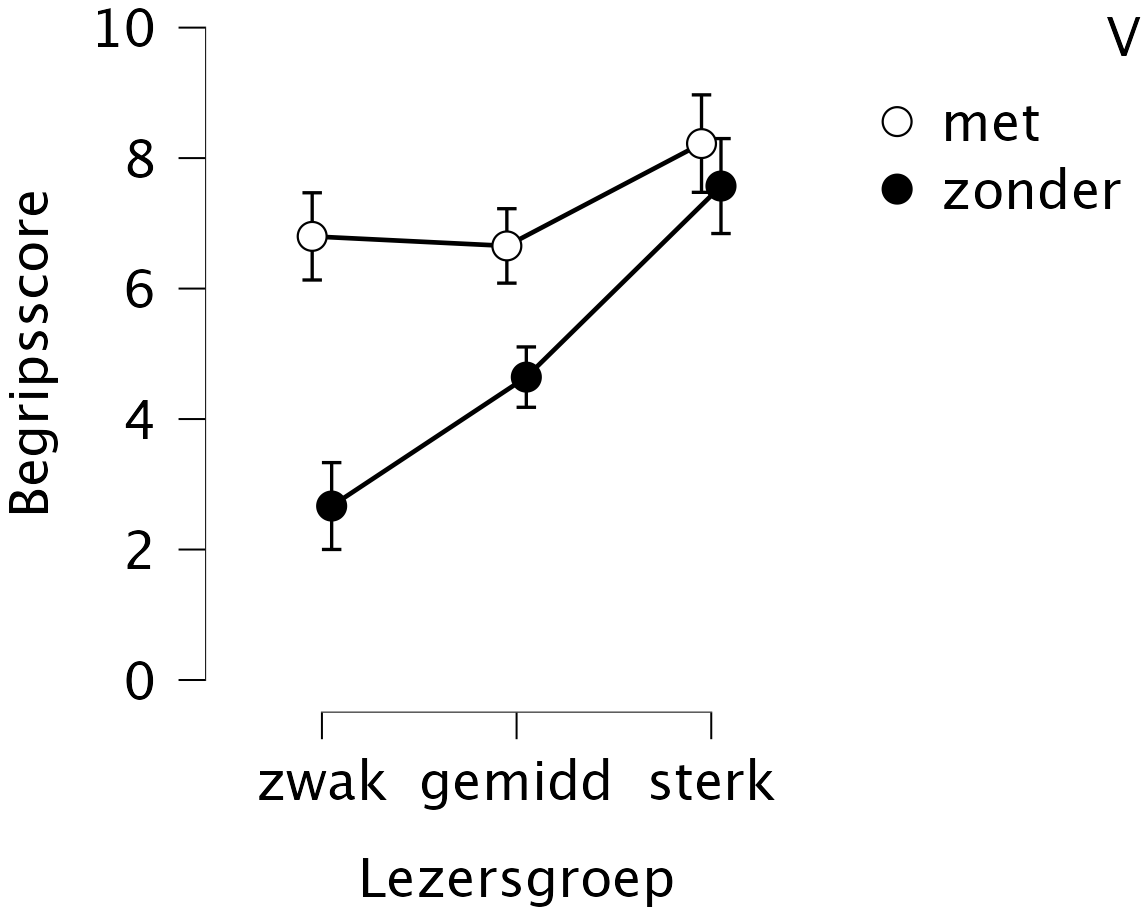
Figuur 15.3: Gemiddelde begripsscores (met 95%-betrouwbaarheidsintervallen), voor twee tekstversies en drie groepen lezers (naar Van Dooren, Van den Bergh en Evers-Vermeul, 2012).

---

Als er een significante interactie aanwezig is, zoals in het bovenstaande voorbeeld, dan kunnen we niet meer algemene uitspraken doen over de betrokken hoofdeffecten. Immers, de werking van een hoofdeffect hangt dan tevens af van de wisselwerking met (een) ander(e) hoofdeffect(en) ³³. In het bovenstaande voorbeeld: het verschil tussen de tekstversies (factor A) is groot voor zwakke lezers, maar nihil voor sterke lezers. Het verschil tussen de lezerstypen (factor B) is groot bij een tekst zonder markeringen, maar veel kleiner bij een tekst met structuurmarkeringen.

Een ander interactie-patroon zagen we al eerder, in Figuur 6.1 (§6.8). De scores zijn gemiddeld niet hoger voor de ene groep luisteraars dan voor de andere groep, en de scores zijn ook niet gemiddeld hoger in de ene conditie dan in de andere. De twee hoofdeffecten zijn dus niet significant, maar hun interactie is daarentegen wel significant. In dat onderzoek is het effect van de ene factor precies tegengesteld in de twee verschillende niveaus van de andere factor.

15.4.2 Een formele uitleg

We nemen wederom aan dat de scores zijn opgebouwd volgens een statistisch model, nl. als de optelsom van het populatiegemiddelde \(\mu\), een systematisch effect \(\alpha_j\) van de \(j\)’de conditie van factor A, een systematisch effect \(\beta_k\) van de \(k\)’de conditie van factor B, een systematisch effect \((\alpha\beta)_{jk}\) van de combinatie van condities \((j,k)\) van factoren A en B, en een toevallig effect \(e_{ijk}\) voor de \(i\)’de replicatie binnen de \(jk\)’de cel. In formule:

\[x_{ijk} = \mu + \alpha_{j} + \beta_{k} + (\alpha\beta)_{jk} + e_{ijk}\]

Bij de éénweg-variantieanalyse wordt de totale ‘sums of squares’ opgesplitst in twee componenten, nl. één tussen en één binnen condities (zie vergelijking (15.4)). Bij de tweeweg-variantieanalyse zijn er nu echter vier componenten, nl. drie tussen condities en één binnen condities (within):

\[\begin{equation} \tag{15.8} { SS_t } = SS_A + SS_B + SS_{AB} + SS_{within} \end{equation}\]

\[\begin{align} \tag{15.9} { \sum (x_{ijk} - \overline{x})^2 } = & { \sum_j n_j (\bar{x}_j - \bar{x})^2 } + \\ & { \sum_k n_k (\bar{x}_k - \bar{x})^2 } + \\ & { \sum_j \sum_k n_{jk} (\bar{x}_{jk} - \bar{x}_j - \bar{x}_k + \bar{x})^2 } + \\ & { \sum_i \sum_j \sum_k (x_{ijk} - \bar{x}_{jk})^2 } \end{align}\]

Ook de vrijheidsgraden van deze kwadratensommen tellen weer bij elkaar op:

\[\begin{equation} \tag{15.10} { \textrm{df}_t } = \textrm{df}_A + \textrm{df}_B + \textrm{df}_{AB} + \textrm{df}_{within} \end{equation}\]

\[\begin{equation} \tag{15.11} { (N-1) } = (A-1) + (B-1) + (A-1)(B-1) + (N-AB) \end{equation}\]

Net als bij de eenweg-variantieanalyse berekenen we weer de ‘mean squares’ door de kwadratensommen te delen door hun vrijheidsgraden.

We toetsen nu drie nulhypotheses, nl voor de twee hoofdeffecten en voor hun interactie. Voor elke toets bepalen we de betreffende \(F\)-ratio. De teller wordt gevormd door de geobserveerde variantie, zoals hierboven geformuleerd; de noemer wordt gevormd door \(s^2_{within}\), de toevallige variantie tussen de replicaties binnen de cellen. Alle noodzakelijke berekeningen voor variantieanalyse, inclusief bepalen van vrijheidsgraden en overschrijdingskansen, worden tegenwoordig door de computer uitgevoerd.

De resultaten worden weer samengevat in een ANOVA-tabel, die nu iets is uitgebreid in Tabel 15.5. We toetsen en rapporteren nu drie hypothesen.

Tabel 15.5: Samenvatting van tweewegs-variantieanalyse van de begripsscores van twee tekstversies en drie lezerstypen.

variantiebron	df	SS	MS	\(F\)	\(p\)
(A) tekstversie	1	91.2663	91.2663	63.75	<.001
(B) lezerstype	2	96.0800	48.0400	33.56	<.001
(C) interactie	2	30.7416	15.3708	10.74	<.001
within	88	125.9830	1.4316

Daarbij rapporteren we doorgaans eerst de hoofdeffecten, en daarna de interactie. Voor de interpretatie is het van belang of de interactie wel of niet significant is. Als de interactie wel significant is, dan rapporteren we eerst de hoofdeffecten zonder die te interpreteren, daarna rapporteren en interpreteren we de interactie, en tenslotte interpreteren we de eventuele significante hoofdeffecten die niet bij de interactie geïnterpreteerd zijn. Als de interactie niet significant is, dan kan het makkelijker zijn om eerst de hoofdeffecten te rapporteren en te interpreteren, en daarna rapporteren we de interactie (die dan niet geïnterpreteerd wordt).

15.4.3 Post-hoc vergelijkingen

Ook bij tweeweg-variantieanalyse kunnen we weer post-hoc vergelijkingen uitvoeren (vgl. §15.3.5) om te onderzoeken welke cellen of combinaties van condities van elkaar verschillen. We gebruiken daarvoor wederom de Tukey HSD toets.

De Tukey HSD toets resulteert in een 95% betrouwbaarheidsinterval van het verschil tussen twee condities, en/of in een \(p\)-waarde van het verschil tussen twee condities.

De begripsscores lieten een significant hoofdeffect zien van de structuurmarkeringen \([F(1,88)=63.75, p<.001, \omega^2=.26]\), alsmede een significant hoofdeffect van het lezerstype \([F(2,88)=33.56, p<.001, \omega^2=.27]\). Ook was er een significante interactie zien tussen de tekstversie en het lezerstype \([F(2,88)=10.74, p<.001, \omega^2=.08]\), zie Figuur 15.3; deze interactie werd nader onderzocht met de Tukey HSD-toets (tussen 6 cellen). Zwakke lezers presteren slechter dan gemiddelde lezers, bij de tekstversie zonder markeringen (p<.001), maar niet bij de versie met markeringen (\(p=.99\)). Sterke lezers presteren beter dan gemiddelde lezers, zowel zonder markeringen (\(p<.001\)) als met markeringen (p=.01). Tekstmarkeringen hebben wel effect bij zwakke lezers (\(p<.001\)) en bij gemiddelde lezers (\(p<.001\)) maar niet bij sterke lezers (\(p=.89\)); sterke lezers hebben dus geen baat bij structuurmarkeringen in de tekst, maar zwakke en gemiddelde lezers wel. Ook interessant is de bevinding dat zwakke lezers een tekst met markeringen net zo goed begrijpen als sterke lezers een tekst zonder markeringen begrijpen (\(p=.72\)).

15.4.4 SPSS

De gegevens voor het bovenstaande voorbeeld zijn te vinden in bestand data/DBE2012.csv.

15.4.4.1 ANOVA

Analyze > General Linear Model > Univariate...

Sleep de afhankelijke variabele (MCBiScore) naar het vakje Dependent variable. Sleep de twee onafhankelijke variabelen (Versie, Groep) naar het vakje Fixed factor(s).

15.4.5 JASP

15.4.5.1 voorbereiding

De gegevens voor het bovenstaande voorbeeld zijn te vinden in bestand data/DBE2012.csv.

Onderzoek of de observaties normaal verdeeld zijn binnen elke groep of cel, met behulp van de technieken uit Deel II van dit tekstboek (met name §10.4). Let op: Dit kan in JASP ook tegelijk met de variantieanalyse zelf, zie hieronder.

15.4.5.2 ANOVA

Klik in de bovenbalk op:

ANOVA > ANOVA (onder 'Classical)

Selecteer de variabele MCBiScore en plaats deze in het veld “Dependent Variable”, en plaats variabelen Versie (tekstversie) en Groep (lezerstype) in het veld “Fixed Factors”.
Zorg dat onder “Display” Estimates of effect size is aangevinkt, en kies hier tussen \(\omega^2\) en/of (partial) \(\eta^2\). In dit boek houden we \(\omega^2\) aan. Je kunt ook Descriptive statistics aanvinken om beschrijvende statistiek van de scores per groep te krijgen. Dit geeft inzicht in wat je aan het testen bent.
Open de balk “Model” en selecteer onderin bij “Sum of squares” Type III.
Open de balk “Assumption Checks” en vink Homogeneity tests aan. “Homogeneity corrections” mag op None blijven staan. Je kunt hier ook onderzoeken of de verdeling binnen iedere groep of cel normaal is, dat is equivalent aan een normale verdeling van de residuen van de variantieanalyse. Dat inspecteer je door hier ook Q-Q plot of residuals aan te vinken; in de resulterende Q-Q-plot zouden de residuen ongeveer op een rechte lijn moeten liggen (zie §10.4).

Open ook de balk “Descriptive Plots” en selecteer variabele Groep in het veld “Horizontal Axis” en variabele Versie in het veld “Separate Lines”.

In de uitvoer wordt de variantieanalyse samengevat in een tabel gelijkend op Tabel 15.5, waarbij ook de effectgrootte vermeld wordt in de vorm van \(\omega^2\) en/of (partial) \(\eta^2\). Onder Descriptive plots zie je een visuele weergave van wat er wordt getoetst; dit helpt om het eventuele interactie-effect beter te begrijpen.

In de uitvoer vind je onder Assumption Checks ook de uitslag van Levene’s toets op gelijke varianties (homogeniteit van variantie), die geen aanleiding geeft om H0 te verwerpen. We mogen dus een variantieanalyse uitvoeren.

15.4.5.3 post-hoc vergelijking

Voor een variantieanalyse met post-hoc vergelijkingen moeten we de gewenste post-hoc vergelijkingen aanvragen. De werkwijze is in het begin hetzelfde als hierboven.

Open vervolgens de balk “Post Hoc Tests” en verplaats de interactie Versie x Groep naar het veld rechts. Zorg dat onder “Type” Standard is aangevinkt en daaronder ook Effect size. Vink onder “Correction” Tukey aan, en onder “Display” ook Confidence intervals.

De uitvoer geeft nu onder Post Hoc Tests de resultaten. Voor iedere paarsgewijze vergelijking tussen de 2x3 cellen zien we het verschil, de standaardfout, en de ondergrens en bovengrens van het 95% betrouwbaarheidsinterval van dat verschil. Als dat interval niet nul omvat, dan is het verschil tussen de twee groepen of condities dus waarschijnlijk niet gelijk aan nul. De gecorrigeerde overschrijdingskans volgens Tukey’s HSD toets is bovendien gegeven in de laatste kolom.

Voor de versie zonder markeringen zien we dat de cel zonder:zwak lager scoort dan de cel zonder:gemiddeld (\(p<.001\)), en dat de cel zonder:sterk hoger scoort dan de cel zonder:gemiddeld (\(p<.001\)). Voor de versie met markeringen zien we dat de cel met:zwak ongeveer gelijk scoort met de cel met:gemiddeld (\(p=.99\)), en dat de cel met:sterk hoger scoort dan de cel met:gemiddeld (\(p=.01\)). Sterke lezers doen het dus beter dan gemiddelde en/of zwakke lezers, bij beide tekstversies. Ook zien we dat zonder:zwak lager scoort dan met:zwak (\(p<.001\)), dat zonder:gemiddeld lager scoort dan met:gemiddeld (\(p<.001\)), terwijl er geen verschil is tussen zonder:sterk en met:sterk (\(p=.89\)). Sterke lezers hebben dus geen baat bij structuurmarkeringen in de tekst. Ook interessant is de bevinding dat zwakke lezers een tekst met markeringen net zo goed begrijpen als sterke lezers een tekst zonder markeringen begrijpen (\(p=.72\)).

15.4.6 R

15.4.6.1 voorbereiding

De gegevens voor het bovenstaande voorbeeld zijn te vinden in bestand data/DBE2012.csv.

DBE2012 <- read.csv(file="data/DBE2012.csv")
# Versie: 1=met, 2=zonder structuurmarkeringen
# Groep: 1=zwak, 2=gemiddeld, 3=sterk
# zorg dat Versie en Groep categorische variabelen of factoren zijn:
DBE2012$Versie <- factor(DBE2012$Versie, labels=c("met","zonder") )
DBE2012$Groep <- factor(DBE2012$Groep, labels=c("zwak","gemiddeld","sterk") )
# DV: MCBiScore: aantal begripsvragen (uit 10) goed beantwoord, over BIO tekst
# tabel van gemiddelden, zie Table 15.2 in hoofdtekst
with( DBE2012, tapply( MCBiScore, list(Versie,Groep), mean ))

##            zwak gemiddeld    sterk
## met    6.800000  6.653846 8.222222
## zonder 2.666667  4.642857 7.571429

15.4.6.2 ANOVA

summary( aov(MCBiScore~Versie*Groep, data=DBE2012) -> DBE2012.m1 )

##              Df Sum Sq Mean Sq F value   Pr(>F)    
## Versie        1 121.18  121.18   84.64 1.59e-14 ***
## Groep         2  81.41   40.71   28.43 2.98e-10 ***
## Versie:Groep  2  30.74   15.37   10.74 6.72e-05 ***
## Residuals    88 125.98    1.43                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

De uitkomsten wijken enigszins af van die in Tabel 15.5 omdat R de Sums of Squares op een andere wijze berekent³⁴.

15.4.6.3 effectgrootte

We gebruiken hiervoor de eerder geprogrammeerde functie omegasq (§15.3.8.3):

omegasq(DBE2012.m1, "Versie")        # [1] 0.33

## [1] 0.3319423

omegasq(DBE2012.m1, "Groep")         # [1] 0.22

## [1] 0.2177437

omegasq(DBE2012.m1, "Versie:Groep")  # [1] 0.08

## [1] 0.07727868

De uitkomsten wijken enigszins af van die in de tekst hierboven omdat R de Sums of Squares op een iets andere wijze berekent.

15.4.6.4 post-hoc toetsen

TukeyHSD(x=DBE2012.m1, which="Versie:Groep")

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = MCBiScore ~ Versie * Groep, data = DBE2012)
## 
## $`Versie:Groep`
##                                      diff         lwr        upr     p adj
## zonder:zwak-met:zwak           -4.1333333 -5.60315087 -2.6635158 0.0000000
## met:gemiddeld-met:zwak         -0.1461538 -1.27642935  0.9841217 0.9989799
## zonder:gemiddeld-met:zwak      -2.1571429 -3.27255218 -1.0417335 0.0000031
## met:sterk-met:zwak              1.4222222 -0.04759532  2.8920398 0.0637117
## zonder:sterk-met:zwak           0.7714286 -0.82423518  2.3670923 0.7218038
## met:gemiddeld-zonder:zwak       3.9871795  2.63899048  5.3353685 0.0000000
## zonder:gemiddeld-zonder:zwak    1.9761905  0.64044018  3.3119408 0.0005900
## met:sterk-zonder:zwak           5.5555556  3.91224959  7.1988615 0.0000000
## zonder:sterk-zonder:zwak        4.9047619  3.14799393  6.6615299 0.0000000
## zonder:gemiddeld-met:gemiddeld -2.0109890 -2.96040355 -1.0615745 0.0000003
## met:sterk-met:gemiddeld         1.5683761  0.22018706  2.9165651 0.0130213
## zonder:sterk-met:gemiddeld      0.9175824 -0.56680056  2.4019654 0.4704754
## met:sterk-zonder:gemiddeld      3.5793651  2.24361478  4.9151154 0.0000000
## zonder:sterk-zonder:gemiddeld   2.9285714  1.45547670  4.4016662 0.0000016
## zonder:sterk-met:sterk         -0.6507937 -2.40756162  1.1059743 0.8883523

Ook hier wijken de uitkomsten enigszins af van die in de tekst hierboven omdat R de Sums of Squares op een iets andere wijze berekent.

Voor iedere paarsgewijze vergelijking tussen de 2x3 cellen zien we het verschil, de ondergrens en bovengrens van het 95%-betrouwbaarheidsinterval van dat verschil, en de gecorrigeerde overschrijdingskans volgens Tukey’s HSD toets.

Voor de versie zonder markeringen zien we dat de cel zonder:zwak lager scoort dan de cel zonder:gemiddeld (\(p<.001\)), en dat de cel zonder:sterk hoger scoort dan de cel zonder:gemiddeld (\(p<.001\)). Voor de versie met markeringen zien we dat de cel met:zwak ongeveer gelijk scoort met de cel met:gemiddeld (\(p=.99\)), en dat de cel met:sterk hoger scoort dan de cel met:gemiddeld (\(p=.01\)). Sterke lezers doen het dus beter dan gemiddelde en/of zwakke lezers, bij beide tekstversies. Ook zien we dat zonder:zwak lager scoort dan met:zwak (p<.001), dat zonder:gemiddeld lager scoort dan met:gemiddeld (p<.001), terwijl er geen verschil is tussen zonder:sterk en met:sterk (p=.89). Sterke lezers hebben dus geen baat bij structuurmarkeringen in de tekst. Ook interessant is de bevinding dat zwakke lezers een tekst met markeringen net zo goed begrijpen als sterke lezers een tekst zonder markeringen begrijpen (\(p=.72\)).

Referenties

Kerlinger, Fred N., and Howard B. Lee. 2000. Foundations of Behavioral Research. 4th ed. Fort Worth: Harcourt College Publishers.

Maxwell, Scott E., and Harold D. Delaney. 2004. Designing Experiments and Analyzing Data: A Model Comparison Perspective. Book. 2nd ed. Mahwah, NJ: Lawrence Erlbaum Associates.

Olejnik, Stephen, and James Algina. 2003. “Generalized Eta and Omega Squared Statistics: Measures of Effect Size for Some Common Research Designs.” Psychological Methods 8 (4): 434–47.

Quene, Hugo. 2022. Hqmisc: Miscellaneous Convenience Functions and Dataset. https://CRAN.R-project.org/package=hqmisc.

Quené, Hugo. 2008. “Multilevel Modeling of Between-Speaker and Within-Speaker Variation in Spontaneous Speech Tempo.” Journal of the Acoustical Society of America 123 (2): 1104–13.

Van Dooren, Wendy, Huub Van den Bergh, and Jacqueline Evers-Vermeul. 2012. “Leesbare Teksten? Over de Invloed van Structuurmarkeringen Op Het Tekstbegrip En Tekstwaardering van Zwakke En Sterke Lezers.” Levende Talen Tijdschrift 13 (4): 31–38. https://lt-tijdschriften.nl/ojs/index.php/ltt/article/view/152.

---

32. Als (1) rood wel verschilt van grijs en blauw, en als (2) grijs en blauw bovendien onderling niet verschillen, dan impliceert dat dat rood verschilt van grijs (een nieuwe bevinding) en dat rood verschilt van blauw (dat wisten we al).↩︎

33. Als we nog meer factoren toevoegen, dan wordt de situatie al snel onoverzichtelijk. Met drie hoofdeffecten zijn er al 3 tweeweg-interacties plus 1 drieweg-interactie. Met vier hoofdeffecten zijn er al 6 tweeweg-interacties, plus 4 drieweg-interacties, plus 1 vierweg-interactie.↩︎

34. De standaard berekeningswijze van R (Type I) is na te bootsen in JASP met de keuze: Model, Sum of squares: Type I. De standaard berekeningswijze van JASP (Type III) is ook na te bootsen in R, zie https://www.r-bloggers.com/2011/03/anova-%E2%80%93-type-iiiiii-ss-explained.↩︎