Hoofdstuk 10 Kansverdelingen

10.1 Kansen

Bellen achter het stuur vergroot de kans op een ongeluk (Bhargava and Pathania 2013). De gemiddelde kans op neerslag in Nederland is 7%. Mijn bestelling heeft 10% kans om een dag later dan beloofd afgeleverd te worden. Kansen en waarschijnlijkheden spelen een belangrijke rol in ons dagelijks leven, en ook in het wetenschappelijk onderzoek. Immers, veel hypothesen zijn probabilistisch van aard (zie Hoofdstuk 2): de hypothesen doen uitspraken over een verschil in kansen van uitkomsten. Om conclusies te kunnen trekken ten aanzien van die probabilistische hypothesen hebben we enige kennis nodig over waarschijnlijkheden, kansberekening, en kansverdelingen. Daarover gaat dit hoofdstuk.

Laten we ter inleiding eens kijken naar een Nederlands Scrabble-spel. Het spel bevat een zakje met daarin 102 fiches, met op elke fiche een letter¹⁹. Van de 102 fiches zijn er 6 met de letter A. Als ik uit een vol en goed gemengd zakje één fiche neem, wat is dan de kans dat ik de letter A tref? Die kans-op-uitkomst-A wordt aangeduid als $P(\textrm{A})$, met de $P$ van Probabilitas (Lat. “kans, waarschijnlijkheid”), en is te bepalen als \[\begin{equation} P(\textrm{A})= \frac{\textrm{aantal A's}}{\textrm{totaal aantal fiches}}= \frac{6}{102} = 0.0588 \tag{10.1} \end{equation}\]

De kans op een gebeurtenis wordt uitgedrukt als een proportie, een getal tussen $0$ en $1$, of als een percentage, d.w.z. een proportie in eenheden van $1/100$. Een kans kan dus nooit kleiner zijn dan $0$ en kan nooit groter zijn dan 1: de kans is immers de verhouding tussen (teller) aantal specifieke uitkomsten en (noemer) totaal aantal mogelijke uitkomsten (zie formule (10.1)), waarbij deze teller nooit groter kan zijn dan deze noemer (Schuurman and De Kluiver 2001).

Als twee uitkomsten elkaar wederzijds uitsluiten, zoals bij de uitkomsten A of B in ons Scrabble-voorbeeld, dan mogen we de kansen van die uitkomsten optellen (somregel). De kans op uitkomst A of uitkomst B (waarbij de uitkomsten A en B elkaar uitsluiten), is de som van $P(\textrm{A})$ en $P(\textrm{B})$: \[\begin{equation} P(\textrm{A of B}) = P(\textrm{A}) + P(\textrm{B}) \tag{10.2} \end{equation}\]

Voorbeeld 10.1: In ons Scrabble-voorbeeld is $P(\textrm{A})=\frac{6}{102}$ en $P(\textrm{B})=\frac{2}{102}$. De kans op uitkomst A-of-B is dan $P(\textrm{A of B})=P(\textrm{A})+P(\textrm{B})=6/102+2/102=8/102=.0784$.

Als ik uit een vol en goed gemengd zakje één fiche neem, dan zijn er twee complementaire uitkomsten mogelijk: ik tref een A, of ik tref niet een A. De uitkomsten sluiten elkaar weer wederzijds uit, dus ook de kansen op deze uitkomsten mogen we optellen. Bovendien zijn de uitkomsten complementair, d.w.z. de uitkomst kan alleen maar één van deze twee mogelijke uitkomsten zijn. De respectievelijke kansen op deze complementaire gebeurtenissen zijn dan ook complementair, d.w.z. deze respectievelijke kansen tellen op tot precies $1$ =100% (complementregel). Er is immers 100% kans dat de uitkomst één van de twee mogelijke uitkomsten van de trekking is. Als we $P(\textrm{A})$ al kennen kunnen we de kans op de complementaire uitkomst makkelijk uitrekenen: \[\begin{align} P(\textrm{A}) + P(\textrm{niet-A}) & = & 1\\ P(\textrm{A}) & = & 1 - P(\textrm{niet-A})\\ P(\textrm{niet-A}) & = & 1 - P(\textrm{A}) \tag{10.3} \end{align}\]

Voorbeeld 10.2: In ons Scrabble-voorbeeld is $P(\textrm{A})=\frac{6}{102}$. De kans op uitkomst niet-A is dan $P(\textrm{niet-A})= 1 - P(\textrm{A}) = 1 - \frac{6}{102} = \frac{96}{102} = .9412$.

Laten we als gedachten-experiment nu een tweede Scrabble-spel pakken, en daaruit een tweede zakje met fiches pakken, eveneens vol en goed gemengd. Uit elk zakje nemen we nu blind één letterfiche. Er zijn nu twee gebeurtenissen of uitkomsten, nl. de uitkomst van de eerste trekking (uit het eerste zakje), en de uitkomst van de tweede trekking (uit het tweede zakje). Deze twee uitkomsten sluiten elkaar niet wederzijds uit, want de twee uitkomsten hebben geen wederzijdse invloed op elkaar. De uitkomst uit het tweede zakje wordt immers niet beïnvloed door de uitkomst van het eerste zakje, of omgekeerd. We zeggen dan dat deze uitkomsten onafhankelijk van elkaar zijn. Als de uitkomsten inderdaad onafhankelijk van elkaar zijn, dan berekenen we de kans op een combinatie van uitkomsten door de kansen te vermenigvuldigen (productregel). De kans op de combinatie van uitkomst A en uitkomst B (waarbij de uitkomsten A en B onafhankelijk van elkaar zijn), is het product van $P(\textrm{A})$ en $P(\textrm{B})$: \[\begin{equation} P(\textrm{A en B}) = P(\textrm{A}) \times P(\textrm{B}) \tag{10.4} \end{equation}\]

Voorbeeld 10.3: In ons Scrabble-voorbeeld is $P(\textrm{A})=\frac{6}{102}$ en $P(\textrm{B})=\frac{2}{102}$. De kans op uitkomst A bij het eerste zakje en B bij het tweede zakje is dan $P(\textrm{A en B})=P(\textrm{A}) \times P(\textrm{B})=\frac{6}{102} \times \frac{2}{102} = .0012$.

Voorbeeld 10.4: In ons Scrabble-voorbeeld is $P(\textrm{klinker})=\frac{38}{102}$. De kans om een klinker (A, E, I, O, U, Y) te trekken uit het eerste zakje en een klinker uit het tweede zakje is dan $P(\textrm{klinker-en-klinker})=P(\textrm{eerste klinker}) \times P(\textrm{tweede klinker})=\frac{38}{102} \times \frac{38}{102} = (\frac{38}{102})^2 = .1388$.

10.2 Binomiale kansverdeling

Voor het vervolg van dit hoofdstuk brengen we twee wijzigingen aan in het Scrabble-spel. Ten eerste verwijderen we de 2 blanco fiches zonder letter uit het zakje. Er blijven dan precies 100 fiches over, waarvan 38 met een klinker (vocaal, $V$) en 62 met een medeklinker (consonant, $C$). Er blijven dus slechts twee mogelijke categorieën van uitkomsten over, die elkaar wederzijds uitsluiten. Zo’n variabele van het nominale meetnivo, met precies twee categorieën, noemen we bi-nomiaal (‘twee-namig’). We beschouwen de klinkers als treffers, en de medeklinkers als missers. Deze twee mogelijke uitkomsten zijn complementair: $P(V)=.38$ (afgekort als $p$) en $P(C)=.62$ (afgekort als $q=1-p$).

Ten tweede leggen we het getrokken letterfiche voortaan terug in het zakje, nadat we de getrokken letter genoteerd hebben. Op die manier hebben we niet tientallen complete letterzakjes nodig, maar slechts één letterzakje dat na elke teruglegging weer compleet en goed gemengd is. We beschouwen de uitkomsten van opeenvolgende trekkingen als onafhankelijk.

Terzijde: De uitkomst van een bepaalde trekking is dus onafhankelijk van de uitkomst van vorige trekkingen. Als er zojuist $100\times$ achtereen een klinker getrokken is, dan heeft dat geen enkele invloed op (de uitkomst van) de eerstvolgende trekking uit het letterzakje. Het letterzakje, of de hand van de trekker, heeft immers geen geheugen. Bij elke trekking is de kans op een treffer $p=.38$, ook als er zojuist $100\times$ of $1000\times$ een klinker is getrokken. Hetzelfde geldt voor de opeenvolgende uitkomsten bij roulette: bij elke ronde is de kans op een treffer $1/37$, ook als het balletje zojuist $100\times$ op eenzelfde getal terecht is gekomen²⁰.

Laten we met bovengenoemde wijzigingen nu $n=3$ trekkingen uitvoeren (met teruglegging, zie boven), en voor elke mogelijke uitkomst de kans op die uitkomst bepalen, zie Tabel 10.1.

Tabel 10.1: Kansen van mogelijke uitkomsten van $n=3$ trekkingen van klinkers, $p=.38$, met teruglegging (zie tekst).
uitkomst	aantal klinkers	kans
CCC	0	$qqq = q^3$
VCC	1	$pqq = pq^2$
CVC	1	$qpq = pq^2$
CCV	1	$qqp = pq^2$
VVC	2	$ppq = p^2q$
VCV	2	$pqp = p^2q$
CVV	2	$qpp = p^2q$
VVV	3	$ppp = p^3$

Het aantal treffers (klinkers) in de $n=3$ trekkingen heeft de kansverdeling zoals samengevat in Tabel 10.2 (eerste en laatste kolom) en Figuur 10.1 (horizontale en verticale as). In zo’n kansverdeling zien we voor elke mogelijke uitkomst van $x$ (hier: aantal klinkers) hoe groot de kans op die uitkomst is.

Tabel 10.2: Kansverdeling van een binomiale variabele met $n=3$ en $p=.38$.
aantal klinkers	kans	kans
0	$1 q^3$	= .2383
1	$3 p q^2$	= .4383
2	$3 p^2 q$	= .2686
3	$1 p^3$	= .0549
som	$(p+q)^3$	= 1.0000

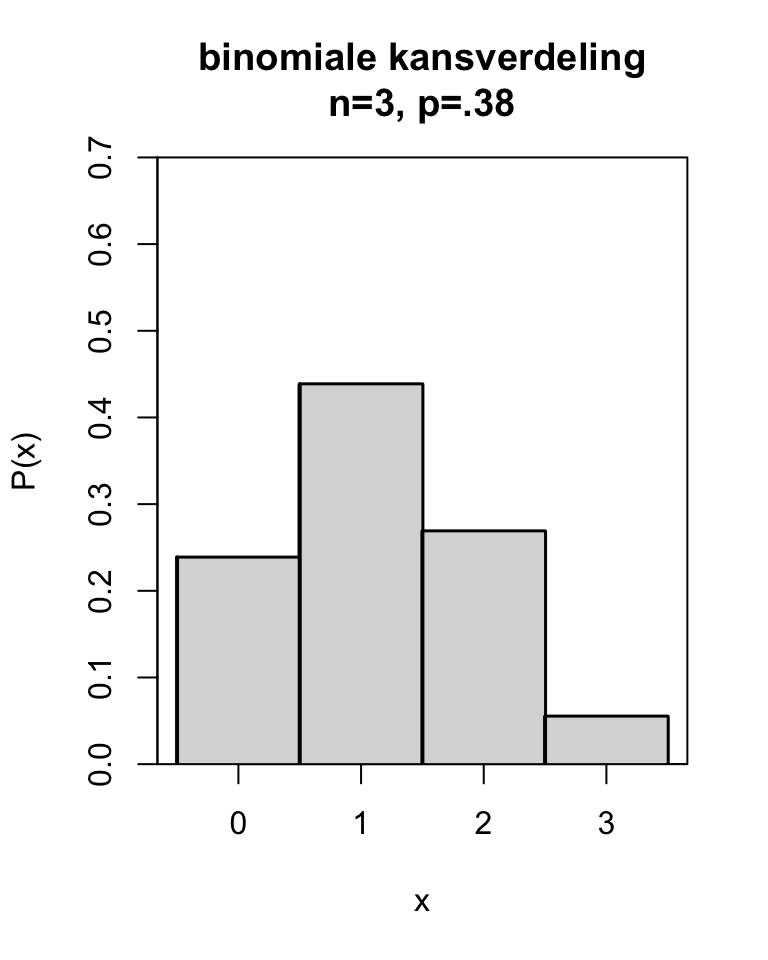
Figuur 10.1: Kansverdeling van een binomiale variabele x met n=3 en p=.38.

De kansverdeling van een binomiale variabele noemen we de binomiale kansverdeling, ook aangeduid als binomiale verdeling of binomiaalverdeling. De exacte kansen van de binomiale kansverdeling kan je uitrekenen met formule (10.5) hieronder.

10.2.1 formules

De kans op een $x$ aantal treffers in $n$ trekkingen is gegeven als \[\begin{equation} P(x\,\mbox{treffers}) = {n \choose x} p^x (1-p)^{n-x} \tag{10.5} \end{equation}\] waarbij $n$ is het aantal trekkingen of pogingen, $x$ is het aantal treffers (tussen 0 en $n$), en $p$ is de kans op een treffer.

De coëfficient ${n \choose x}$ geeft het aantal verschillende ordeningen aan waarin we een combinatie (greep) van $x$ elementen uit $n$ kunnen kiezen. Bij $x=1$ klinker uit $n=3$ trekkingen zijn er drie mogelijkheden: de ene klinker zou getrokken kunnen zijn in de eerste trekking, of de tweede trekking, of de derde trekking, zie Tabel 10.1. Het aantal verschillende mogelijke ordeningen is gegeven als \[\begin{equation} {n \choose x} = \frac{n!}{x!(n-x)!} \tag{10.6} \end{equation}\] waarbij $x! = x (x-1) (x-2) \dots \times 2 \times 1$, dus $4!=4\times3\times2\times1=24$.

Voorbeeld 10.5: Er staan 4 stoelen voor 2 personen. Op een stoel mag maximaal 1 persoon plaatsnemen. Hoeveel verschillende ordeningen van $x=2$ personen over $n=4$ stoelen zijn er mogelijk?

Antwoord: Er zijn ${4 \choose 2} = \frac{4\times3\times2\times1}{2\times1\times2\times1} = \frac{24}{4} = 6$ mogelijke ordeningen, namelijk 1100, 1010, 1001, 0110, 0101, en 0011.

Deze binomiaal-coëfficienten, die het aantal verschillende mogelijke ordeningen aangeven, zijn snel terug te vinden in de zogenaamde Driehoek van Pascal, afgebeeld in Tabel 10.3. Het aantal verschillende ordeningen van $x=2$ personen over $n=4$ stoelen vinden we in rij $n=4$. De bovenste rij is die voor $n=0$. De vijfde rij is die voor $n=4$ en we zien daar achtereenvolgens de binomiaal-coëfficienten voor $x= 0, 1, 2, 3, 4$. Voor ${4 \choose 2}$ vinden we daar de binomiaalcoëfficient $6$. Iedere coefficiënt is de som van de twee bovenliggende coëfficienten²¹, en iedere coëfficient is op te vatten als het aantal mogelijke wegen afdalend van de top van de driehoek naar die cel.

Tabel 10.3: Driehoek van Pascal: binomiaalcoëfficienten voor het aantal mogelijke ordeningen voor een combinatie van $x$ elementen uit $n$ (zie tekst).
$n= 0$:								1
$n= 1$:							1		1
$n= 2$:						1		2		1
$n= 3$:					1		3		3		1
$n= 4$:				1		4		6		4		1
$n= 5$:			1		5		10		10		5		1
$n= 6$:		1		6		15		20		15		6		1
$n= 7$:	1		7		21		35		35		21		7		1

Het gemiddelde en de standaarddeviatie van de binomiale kansverdeling zijn \[\begin{aligned} \mu & = & np \\ \sigma & = & \sqrt{ np(1-p) }\end{aligned}\]

Voorbeeld 10.6: De binomiale kansverdeling voor $x$ treffers uit $n=3$ trekkingen met $p=.38$ kans op een treffer is afgebeeld in Figuur 10.1. Deze binomiale kansverdeling heeft een gemiddelde $\mu=n \times p = 3 \times .38 = 1.14$, en een standaarddeviatie $\sigma = \sqrt{n \times p \times (1-p)} = \sqrt{ 3 \times .38 \times .62} = 0.84$ .

10.2.2 JASP

De binomiale kansverdeling van Figuur 10.1 kan in JASP worden verkregen door in de bovenbalk te klikken op:

Distributions > Binomial (onder 'Discrete')

Als Distributions nog niet in de bovenbalk staat kun je dit toevoegen door rechtsbovenin op de blauwe +-button te klikken en Distributions aan te vinken. In de “Binomial” invoer is de balk Show Distribution als het goed is open. Pas hier de waarden voor $p$ (onder “free parameter”) en $n$ (onder “Fixed parameter”) aan naar $p=0.38$ en $n=3$. Pas onder “Options” ook de range aan naar Range of x from 0 to 3. Onder “Display” moet Probability mass function aangevinkt zijn. In de uitvoer zie je onder Probability Mass Plot de binomiale kansverdeling.

10.2.3 R

dbinom( 0:3, size=3, prob=.38 )

## [1] 0.238328 0.438216 0.268584 0.054872

De uitvoer is weergegeven in Tabel 10.2 hierboven.

matrixcalc::pascal.matrix( 10 ) # links onder diagonaal is Driehoek van Pascal

##       [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
##  [1,]    1    0    0    0    0    0    0    0    0     0
##  [2,]    1    1    0    0    0    0    0    0    0     0
##  [3,]    1    2    1    0    0    0    0    0    0     0
##  [4,]    1    3    3    1    0    0    0    0    0     0
##  [5,]    1    4    6    4    1    0    0    0    0     0
##  [6,]    1    5   10   10    5    1    0    0    0     0
##  [7,]    1    6   15   20   15    6    1    0    0     0
##  [8,]    1    7   21   35   35   21    7    1    0     0
##  [9,]    1    8   28   56   70   56   28    8    1     0
## [10,]    1    9   36   84  126  126   84   36    9     1

De driehoek van Pascal is te vinden links onder de diagonaal van deze matrix.

10.3 Normale kansverdeling

Naarmate de steekproefgrootte $n$ toeneemt, gaat de binomiale kansverdeling minder trapsgewijs verspringen, en wordt de kansverdeling meer vloeiend, zoals te zien in Figuur 10.2.

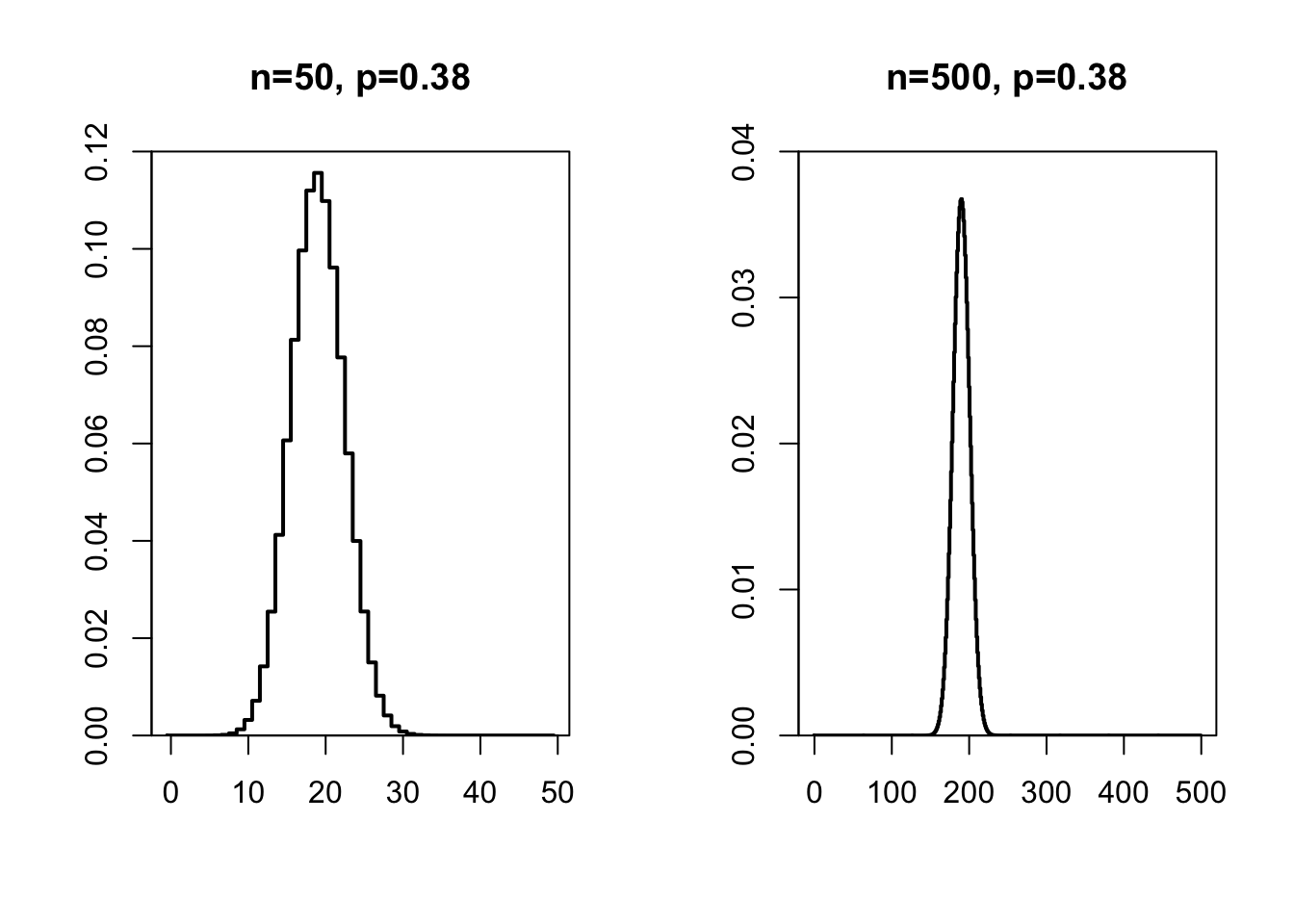
Figuur 10.2: Kansverdeling van een binomiale variabele x met n=50 (links) en n=500 (rechts) en p=.38.

Bij een nog grotere steekproef wordt de kansverdeling een vloeiende lijn. Deze kansverdeling komt zo vaak voor, dat dit de normale kansverdeling of ‘normale verdeling’ wordt genoemd. De verdeling wordt ook wel aangeduid als de Gaussische verdeling (vernoemd naar de wiskundige Carl Friedrich Gauss, 1777–1855), of de ‘bell curve’ (naar de vorm). Heel veel variabelen volgen bij benadering deze kansverdeling: geboortegewicht, lichaamslengte, omvang van woordenschat, IQ, inhoud van een pak melk van 1 liter ℮, duur van een telefoongesprek, enz enz. Voor al deze variabelen hebben observaties dicht bij het gemiddelde een hoge kans om voor te komen, en observaties die sterk afwijken van het gemiddelde zijn relatief zeldzaam (lage kans).

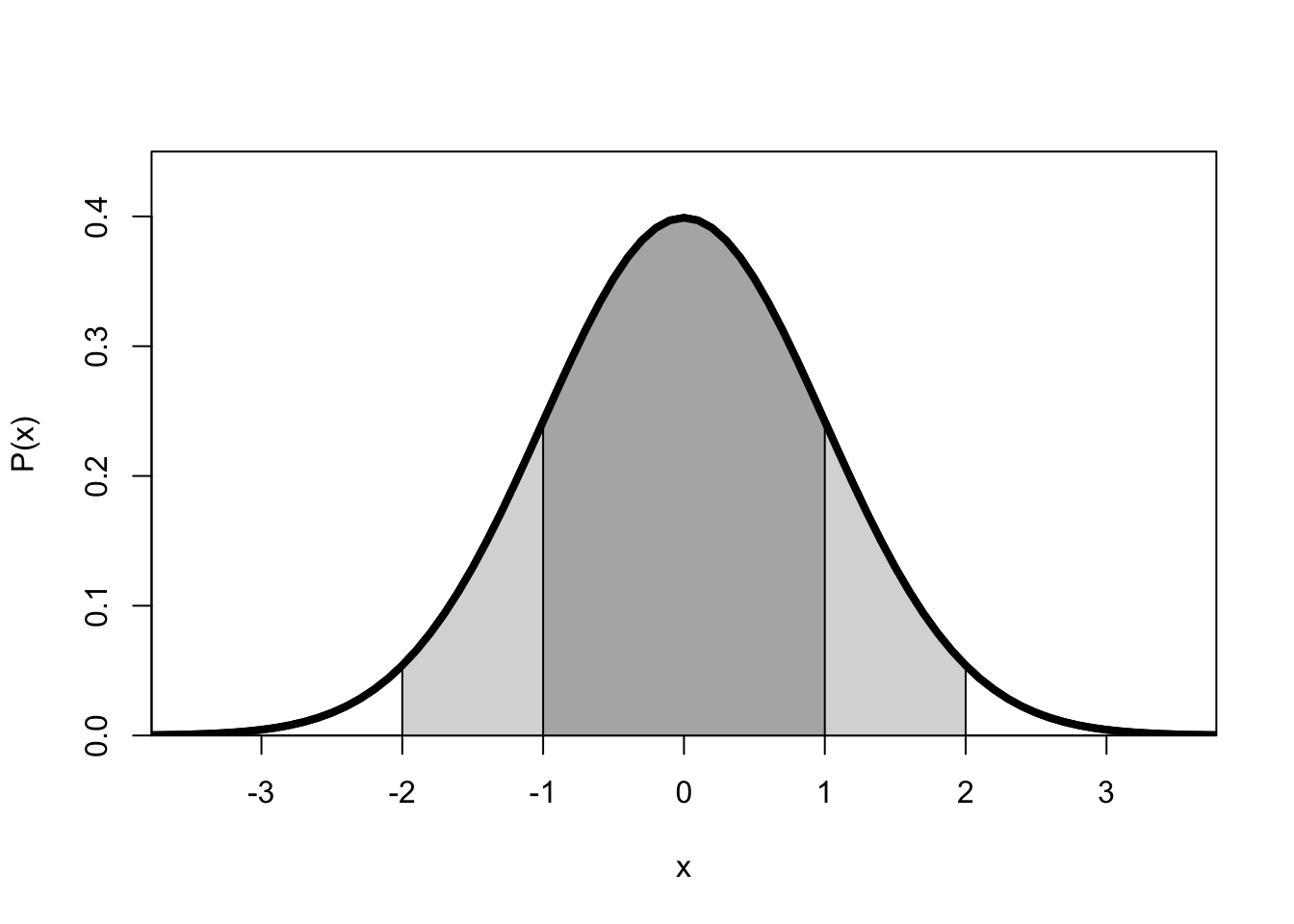
Figuur 10.3: Normale kansverdeling van een variabele x met gemiddelde 0 en standaarddeviatie 1.

De normale kansverdeling van variabele $X$ met gemiddelde $\mu$ en standaarddeviatie $\sigma$ heeft de volgende kenmerken (zie Figuur 10.3):

de verdeling is symmetrisch rond het gemiddelde $\mu$,
de verdeling is asymptotisch, d.w.z. de staarten lopen eindeloos door,
het gemiddelde, de mediaan en de modus vallen samen,
de totale oppervlakte onder de curve, d.i. de totale kans op één van de mogelijke uitkomsten, is gelijk aan 1,
de oppervlakte onder de curve geeft de kans aan op een waarde van $X$ binnen een bepaald interval,
de buigpunten van de curve (van hol naar bol en v.v.) liggen bij $X=\mu-\sigma$ en $X=\mu+\sigma$,
ongeveer 2/3 van de observaties ligt tussen $X=\mu-\sigma$ en $X=\mu+\sigma$ (donkergrijs gebied; $P(-1<x/\sigma<1)=.6827$ of 68%) en ongeveer 95% van de observaties ligt tussen $-2\sigma$ en $+2\sigma$ (donkergrijs plus lichtgrijze gebieden; $P(-2<x/\sigma<2)=.9546$), dit staat bekend als de Empirical Rule.

Een normale kansverdeling met $\mu=0$ en $\sigma=1$ wordt aangeduid als de standaard-normale kansverdeling. Zoals we al eerder zagen (§9.8) kunnen we een normaal-verdeelde variabele $x$ standaardiseren, d.w.z. de observaties transformeren naar een standaardscore of $z$-score: $z = (x-\overline{x})/s$. De kansverdeling in Figuur 10.3 is die van de standaard-normale kansverdeling van $Z$, oftewel de kansverdeling van $(X-\mu)/\sigma$.

De kansverdeling van een normaal verdeelde variabele $X$ zou je zelf kunnen uitrekenen met behulp van formule (10.8) hieronder. Maar het is handiger om daarvoor een tabel te gebruiken; die staat in Bijlage B. In grafische vorm uitgelegd geven die tabellen je, voor verschillende oppervlakten ofwel kansen $p$ aan de rechter zijde onder de curve, de positieve waarde van $Z^*$ die de linkergrens vormt van die oppervlakte. Dat betekent dus dat je precies de kans $p$ hebt om een waarde te vinden van $Z$ die even groot als of groter dan deze ondergrens $Z^*$ is (mits de variabele inderdaad normaal verdeeld is).

Voorbeeld 10.7: Aan de rechterzijde van Figuur 10.3 zien we een klein wit oppervlak onder de curve. Dit oppervlak geeft de kans weer dat $Z>2$. Het oppervlak heeft een omvang van 0.0228. De kans om een waarde van $Z>2$ te vinden is dus 0.0228 ofwel iets minder dan 2.5%. (Tip: relateer deze kans aan de bovengenoemde Empirical Rule).

In Bijlage B vind je gemakshalve niet een maar twee tabellen, elk bestaande uit meerdere kolom-aanduidingen en één rij van cellen. De eerste tabel geeft je, voor verschillende ‘afgeronde’ kansen $p$ (kolommen), de kritieke waarde $Z^*$ (cellen) waarvoor geldt dat de kans $p$ om een waarde van $Z$ te vinden die even groot als of groter dan deze kritieke waarde $Z^*$ is, precies gelijk is aan de waarde $p$ bovenaan de kolom. De tweede tabel werkt net zo, maar dan voor ‘afgeronde’ waarden van $Z^*$ in de cellen, en precieze kansen $p$ in de kolom-aanduidingen.

Wat is de kans $p$ dat $Z>1$? In de tweede deeltabel, tweede kolom, vinden we $p=0.1587$. We weten daarmee ook dat $P(Z<1)$ wel $1-0.1587=0.8413$ moet zijn. Bovendien weten we dat de verdeling symmetrisch is (zie hierboven), dus weten we dat $P(Z< -1)$ ook $.1587$ moet zijn. Wat is de kans $p$ dat $Z>3$ is? In de tweede deeltabel vinden we voor grenswaarde $Z^*=3$ de overschrijdingskans $p=0.0013$. Voor een normaal verdeelde variabele $Z$ is er dus een overschrijdingskans $p=0.0013$ (meestal gerapporteerd als $p=.001$) om een waarde van $Z$ te vinden die tenminste drie standaarddeviaties boven het gemiddelde ligt.

Vaak willen we het omgekeerde weten: als we een bepaalde overschrijdingskans kiezen, welke grenswaarde $Z^*$ hoort daar dan bij? Welke grenswaarde onderscheidt de hoogste 5% van de observaties van de onderste 95% ($p=0.05$)? In de eerste deeltabel vinden we voor overschrijdingskans $p=0.05$ de grenswaarde $Z^*=1.645$. Deze grenswaarde, teruggerekend naar de oorspronkelijke variabele, wordt dan vaak aangeduid als het 95e percentiel of ‘P95’ van de verdeling. Wie tenminste deze score heeft behaald, behoort bij de beste 5% en heeft het dus beter gedaan dan 95% van de deelnemers.

Voorbeeld 10.8: Extreme waarden komen bij een normaal-verdeelde variabele per definitie weinig voor. Maar wat is de grens voor een extreme waarde? Laten we aannemen dat we niet meer dan 5% van alle observaties als extreem willen beschouwen. De normale kansverdeling is symmetrisch, dus van die 5% is te verwachten dat de ene helft (2.5%) ligt aan het linker uiteinde van de verdeling, en de andere 2.5% aan de rechterzijde. Welke grenswaarde $Z^*$ correspondeert met deze overschrijdingskans $p=0.025$?

In Bijlage @ref(app- kritiekeZwaarden) nemen we de eerste deeltabel. In de kolom voor overschrijdingskans $p=0.025$, vinden we grenswaarde $Z^*=1.960$. Als we een observatie vinden met $Z \ge 1.960$ of met $Z \le -1.960$ dan beschouwen we dat als een extreme, zeldzame observatie.

Voorbeeld 10.9: Intelligentie wordt uitgedrukt als een IQ-score, een variabele met een normale kansverdeling met $\mu=100$ en $\sigma=15$. “Membership of Mensa is open to persons who have attained a score within the upper two percent of the general population on an approved intelligence test that has been properly administered and supervised” (www.mensa.org). Welke IQ-score moet je tenminste behalen om lid te kunnen worden?

Antwoord: Het 98e percentiel van een standaard-normaal verdeelde variabele ligt bij $Z^*=+2.0537$, en dus met $x=\overline{x}+2.0537 s = 100+30.8 = 130.8$. Naar boven afgerond moet je dus een IQ-score behalen van 131 punten of hoger.

Voorbeeld 10.10: Verifieer de bovengenoemde Empirical Rule met behulp van Bijlage B.

10.3.1 formules

Als variabele $X$ een normale kansverdeling heeft, met gemiddelde $\mu$ en standaarddeviatie $\sigma$, dan wordt dat aangegeven als \[\begin{equation} X \sim \mathcal{N}(\mu,\sigma) \tag{10.7} \end{equation}\]

De normale kansverdeling van variabele $X$ met gemiddelde $\mu$ en standaarddeviatie $\sigma$ is \[\begin{equation} P(X) = \frac{1}{\sigma \sqrt{2\pi}} \mbox{e}^{ \frac{-(X-\mu)^2}{2\sigma^2} }. \tag{10.8} \end{equation}\]

De standaard-normale kansverdeling van variabele $Z$ met gemiddelde $\mu=0$ en standaarddeviatie $\sigma=1$ is \[\begin{equation} P(Z) = \frac{1}{\sqrt{2\pi}} \mbox{e}^{ \frac{-Z^2}{2} } \tag{10.9} \end{equation}\]

10.3.2 JASP

De normale kansverdeling van Figuur 10.3 kan in JASP worden verkregen door in de bovenbalk te klikken op:

Distributions > Normal (onder 'Continuous')

Als Distributions nog niet in de bovenbalk staat kun je dit toevoegen door rechtsbovenin op de blauwe +-button te klikken en Distributions aan te vinken.
In de “Normal” invoer is de balk Show Distribution als het goed is open. Automatisch staan de waarden voor de standaard-normale kansverdeling al ingevuld en Probability density function aangevinkt; je ziet deze verdeling dus meteen in de uitvoer onder Density Plot.
Voor andere normale kansverdelingen kunnen de waarden voor $\mu$ en $\sigma$ worden aangepast, en ook de range die wordt weergegeven (onder “Options”). Let op dat je bij “Parameters” $\mu$, $\sigma$ selecteert als je het gemiddelde en de standaarddeviatie ingeeft (voor de standaard-normale kansverdeling maakt dit niet uit, want bij $\sigma=1$ geldt ook $\sigma^2=1$).

10.3.3 R

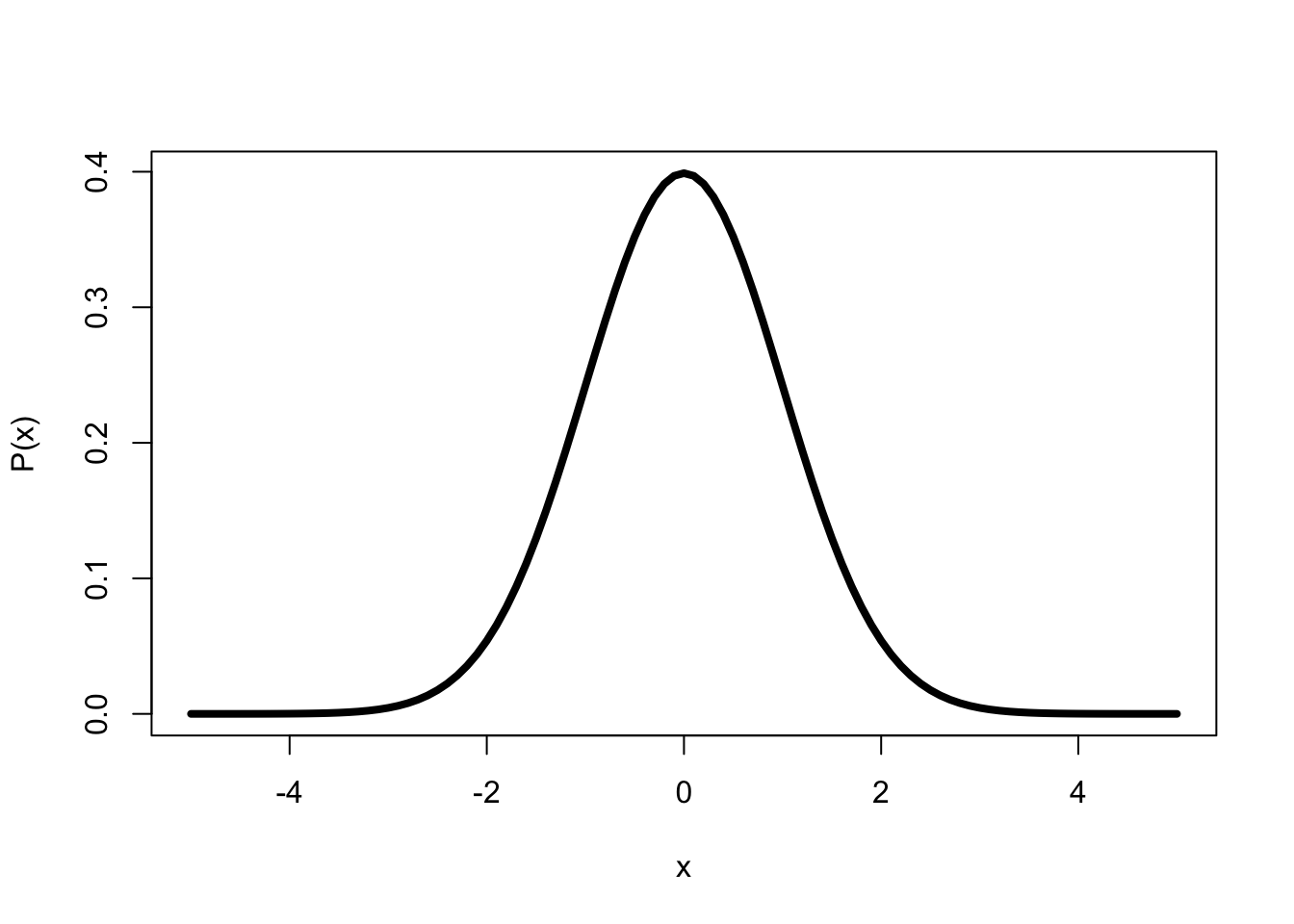
De normale kansverdeling van Figuur 10.3 kan in R worden afgebeeld met het onderstaande commando. Hierin wordt een curve getekend, met x in het aangegeven domein, en waarbij y het resultaat is van de functie die de normale kansverdeling berekent volgens formule (10.8):

curve( dnorm( x, mean=0, sd=1 ), # functie die y-waarden geeft, normal density
       from=-5, to=+5, # domein van x
       lwd=4, # line width is 4x normaal
       xlab="x", ylab="P(x)" # labels langs x-as en y-as
       )

Als je een extra argument curve( ..., add=TRUE ) opgeeft, dan wordt de curve toegevoegd aan de meest recente plot (zie bijv. Figuur 10.6 hieronder).

10.4 Heeft mijn variabele een normale kansverdeling?

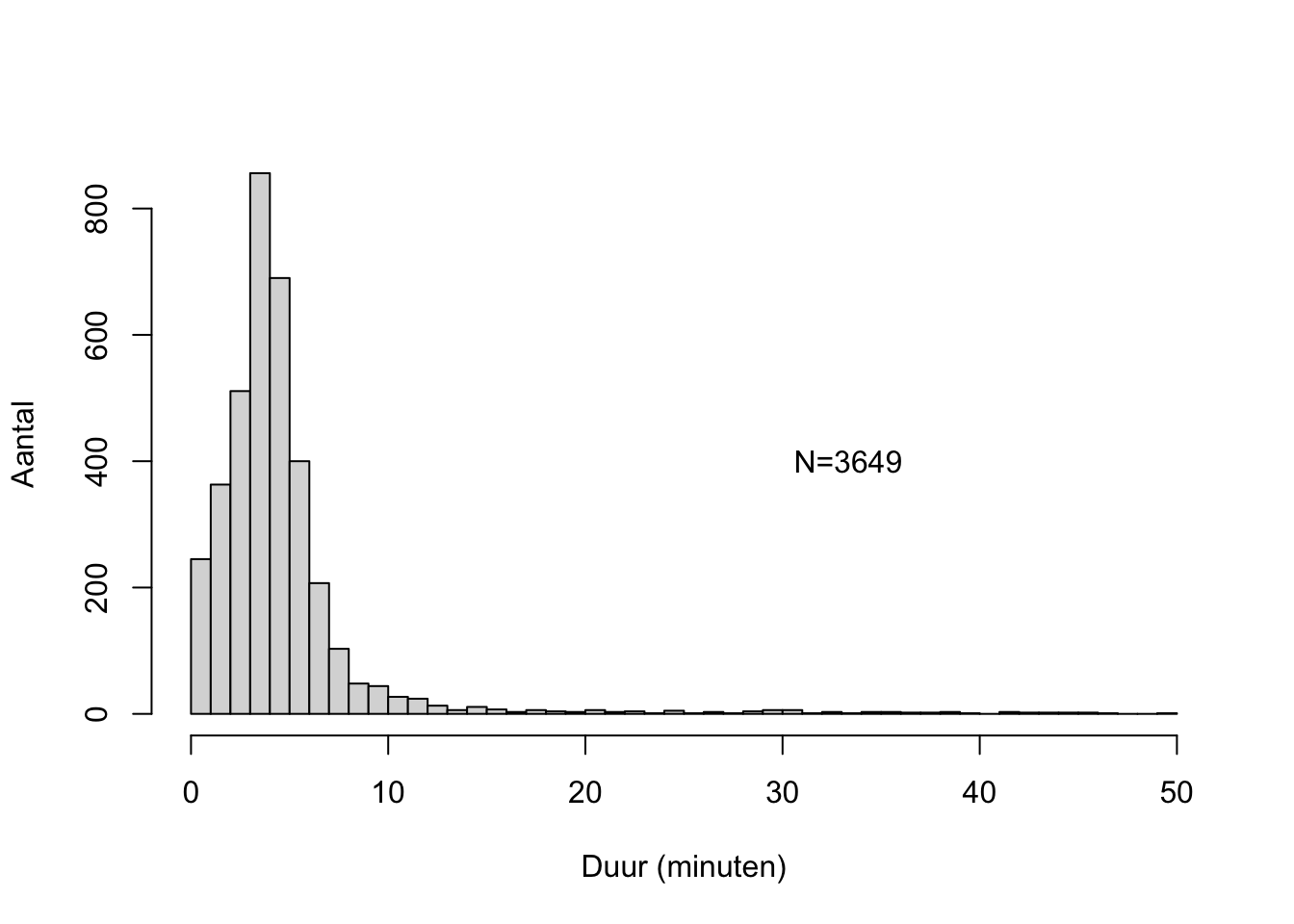
Het langste nummer in mijn digitale muziekbibliotheek duurt ongeveer 50 minuten (dat is een klassiek-indiaas muziekstuk, een ‘morning raga’). Een histogram van de duren van alle muzieknummers zie je in Figuur 10.4.

Figuur 10.4: Histogram van de duren van muzieknummers in mijn digitale muziekbibliotheek.

Dit histogram laat zien dat deze duren duidelijk niet een normale kansverdeling volgen: de verdeling is niet symmetrisch, en de onderste staart loopt niet eindeloos door (er zijn geen muzieknummers met negatieve duren).

Ook het gemiddelde $\bar{x} =$ 4.698 en standaarddeviatie $s =$ 5.11 wijzen op een niet-normale kansverdeling: bij een normale verdeling verwachten we dat slechts $(68/2)+50=84$% van de duren langer duurt dan $\bar{x}-s\approx 0$ minuten, maar in werkelijkheid duurt 100% (dus een groter deel dan verwacht) langer dan 0 minuten.

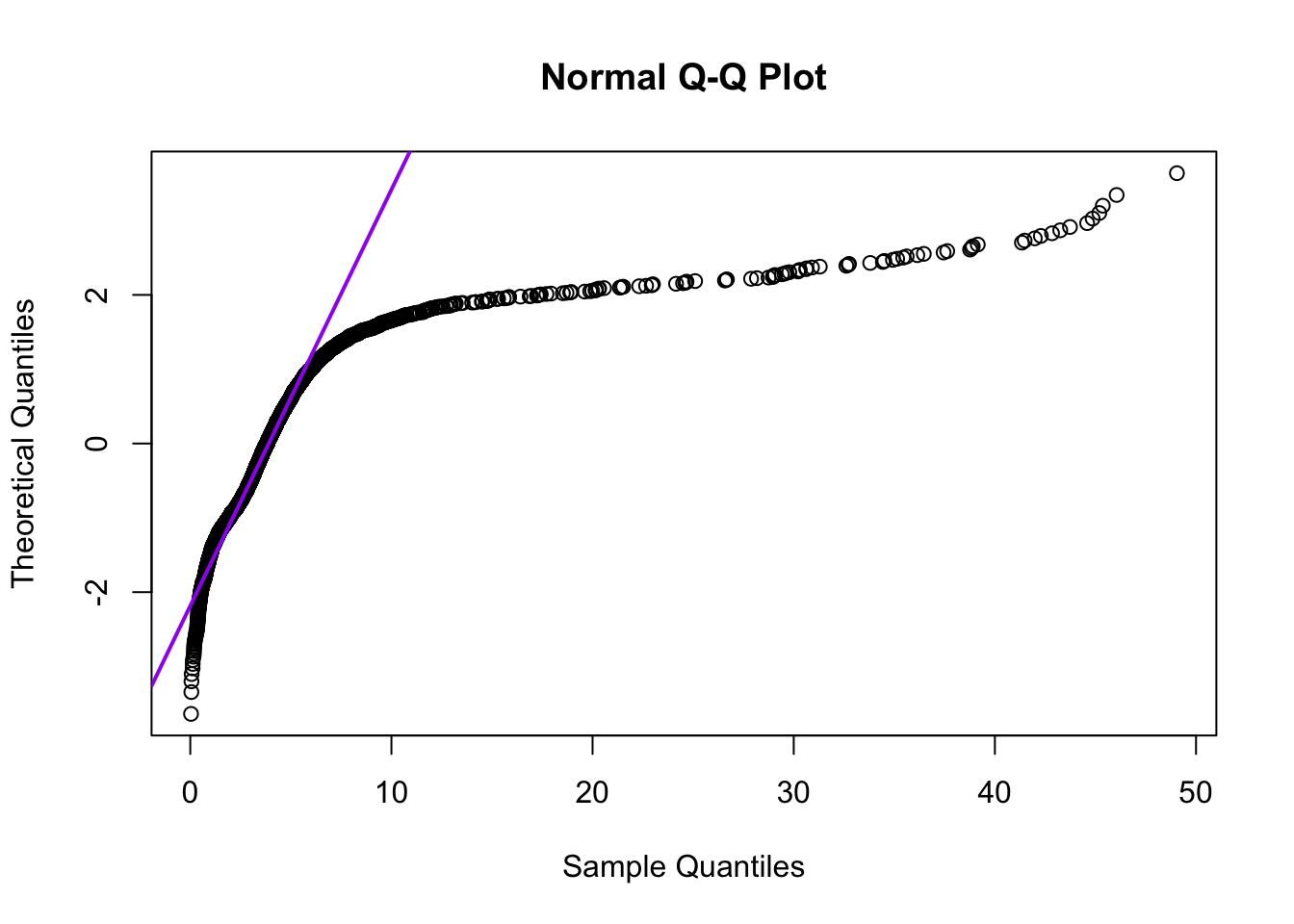
Een veel gebruikte manier om te inspecteren of een variabele $X$ een normale kansverdeling heeft, is om een grafiek te maken met de geobserveerde waarden langs de ene as (hier de horizontale), en de corresponderende $z$-scores langs de andere as. Zo’n figuur wordt een quantile-quantile-plot of QQ-plot genoemd; de QQ-plot voor de duren in mijn muziekbibliotheek zie je in Figuur 10.5.

Figuur 10.5: Quantile-quantile-plot van de duren van muzieknummers in mijn digitale muziekbibliotheek.

Als de duren een normale kansverdeling zouden hebben (normaal zouden zijn verdeeld), dan zouden er een aantal negatieve duren moeten zijn, en er zouden dan veel meer duren tussen 8 en 14 minuten moeten zijn (i.p.v. tussen 8 en 50 minuten). De afwijkingen van de rechte lijn in Figuur 10.5 geven dus aan dat de geobserveerde duren niet een normale kansverdeling volgen, zoals we al zagen in het histogram (Figuur 10.4).

Er zijn ook verschillende statistische toetsen om te onderzoeken of een variabele een normale kansverdeling heeft. De twee meest gebruikte zijn de Shapiro-Wilk-toets (met toetsingsgrootheid $W$) voor normaliteit, en de Kolmogorov-Smirnov-toets (met toetsingsgrootheid $D$) voor normaliteit. Beide toetsen onderzoeken de H0:$X\sim\mathcal{N}(\bar{X},s)$ (zie formule (10.7)).

10.4.1 SPSS

Analyze > Descriptive Statistics > Explore...

Selecteer variabele Time (sleep naar Dependent List paneel).
Kies knop Plots, en vink aan Normality plots with tests, dat betekent ‘als je een QQ-plot oftewel Normality plot maakt, voer dan ook toetsen op normaliteit uit’. Bevestig met Continue en daarna met OK. De uitvoer bevat eerst de resultaten van de Shapiro-Wilks-toets en de Kolmogorov-Smirnov toets. Volgens beide toetsen is de kans om deze verdeling te vinden, als H0 waar is, bijna nul — zie echter de waarschuwing in §13.3! We verwerpen daarom H0 en concluderen dat de duren van muzieknummers niet normaal verdeeld zijn. Na deze toetsresultaten volgt o.a. een QQ-plot.

10.4.2 JASP

Klik in de bovenbalk op Descriptives en selecteer variabele Time in het veld “Variables”. Klik de balk Plots open en vink Distribution plots aan onder “Basic plots” voor een histogram. Vink ook Q-Q plots aan voor een quantile-quantile plot. Klik vervolgens de balk Statistics open en vink Shapiro-Wilk test aan onder “Distribution”.
De uitvoer geeft de uitkomst van de Shapiro-Wilk-toets in de tabel Descriptive Statistics. We zien dat de kans om deze verdeling te vinden, als H0 waar is, bijna nul is. H0 wordt dus verworpen en we concluderen dat de duren van de muzieknummers niet normaal verdeeld zijn. Dit kun je ook terugzien in het histogram en de Q-Q plot.

10.4.3 R

itunes <- read.table( file="data/itunestimes20120511.txt", header=TRUE )
# Size in bytes, Time in ms
qqnorm(itunes$Time/60000, datax=T, plot.it=FALSE) # normally we'd use plot.it=TRUE  
# qqline(itunes$Time/60000, datax=T, col="purple", lwd=T) # see QQ-plot above

shapiro.test(itunes$Time/60000)

## 
##  Shapiro-Wilk normality test
## 
## data:  itunes$Time/60000
## W = 0.50711, p-value < 2.2e-16

Volgens deze toets is de kans om deze verdeling te vinden, als H0 waar is, bijna nul, nl. kleiner dan $2.2 \times 10^{-16}$ (d.i. kleiner dan het kleinste getal dat het analysepakket hier kan weergeven). We verwerpen daarom H0 en concluderen dat de duren van muzieknummers niet normaal verdeeld zijn.

10.5 Wat als mijn variabele niet normaal verdeeld is?

In Deel III zullen we diverse statistische toetsen bespreken. De toetsen die we bespreken in hoofdstukken 13 en 14 en 15 vereisen echter dat de afhankelijke variabele een normale kansverdeling heeft. Als een variabele niet een (ongeveer) normale kansverdeling heeft, dan kan die variabele dus niet zomaar gebruikt worden voor statistische toetsing met de daar behandelde statistische toetsen, of exacter gezegd, de conclusies uit zo’n statistische toetsing zijn dan niet valide. Wat te doen? Er zijn dan twee mogelijkheden.

Ten eerste is het mogelijk om de afhankelijke variabele $y$ te transformeren, d.w.z. dat we er een rekenkundige bewerking op loslaten. Als het goed is, resulteert dat in een variabele $y'$ die wèl bij benadering normaal verdeeld is. Veel gebruikte transformaties zijn: logaritmiseren ($y'=\log{y}$), worteltrekken ($y'=\sqrt{y}$), of inverteren ($y'=1/y$). Vervolgens wordt de getransformeerde afhankelijke variabele $y'$ gebruikt voor de statistische toetsing. Uiteraard moet je wel controleren of de nieuwe afhankelijke variabele $y'$ inderdaad (bij benadering) normaal verdeeld is. Ook moet je bij de interpretatie van de resultaten van de analyse rekening houden met de uitgevoerde transformatie!

Ten tweede is het soms mogelijk om een andere statistische toets te gebruiken, die niet vereist dat de afhankelijke variabele normaal verdeeld is. Dat worden non-parametrische toetsen genoemd. We gaan er nader op in in de hoofdstukken 16 en 17. Die toetsen hebben wel als nadeel dat ze minder statistische power hebben (voor een bespreking van power, zie hoofdstuk 14): ze zijn minder gevoelig, en vereisen dus grotere steekproeven om een effect vast te stellen.

10.6 Kansverdeling van gemiddelde

In deze paragraaf beschouwen we de muzieknummers in mijn digitale muziekbibliotheek als een populatie. We nemen nu een willekeurige steekproef van $n=$ 50 nummers, en bepalen de gemiddelde duur over deze 50 muzieknummers in de steekproef: stel $\bar{x} =$ 4.401 minuten. Opvallend genoeg ligt dit gemiddelde van de steekproef dicht bij het gemiddelde van de populatie ($\mu =$ 4.615 minuten, zie hierboven). Deze operatie herhalen we $250\times$: we krijgen zo 250 steekproefgemiddelden. De frequentieverdeling van die 250 steekproefgemiddelden zie je in Figuur 10.6.

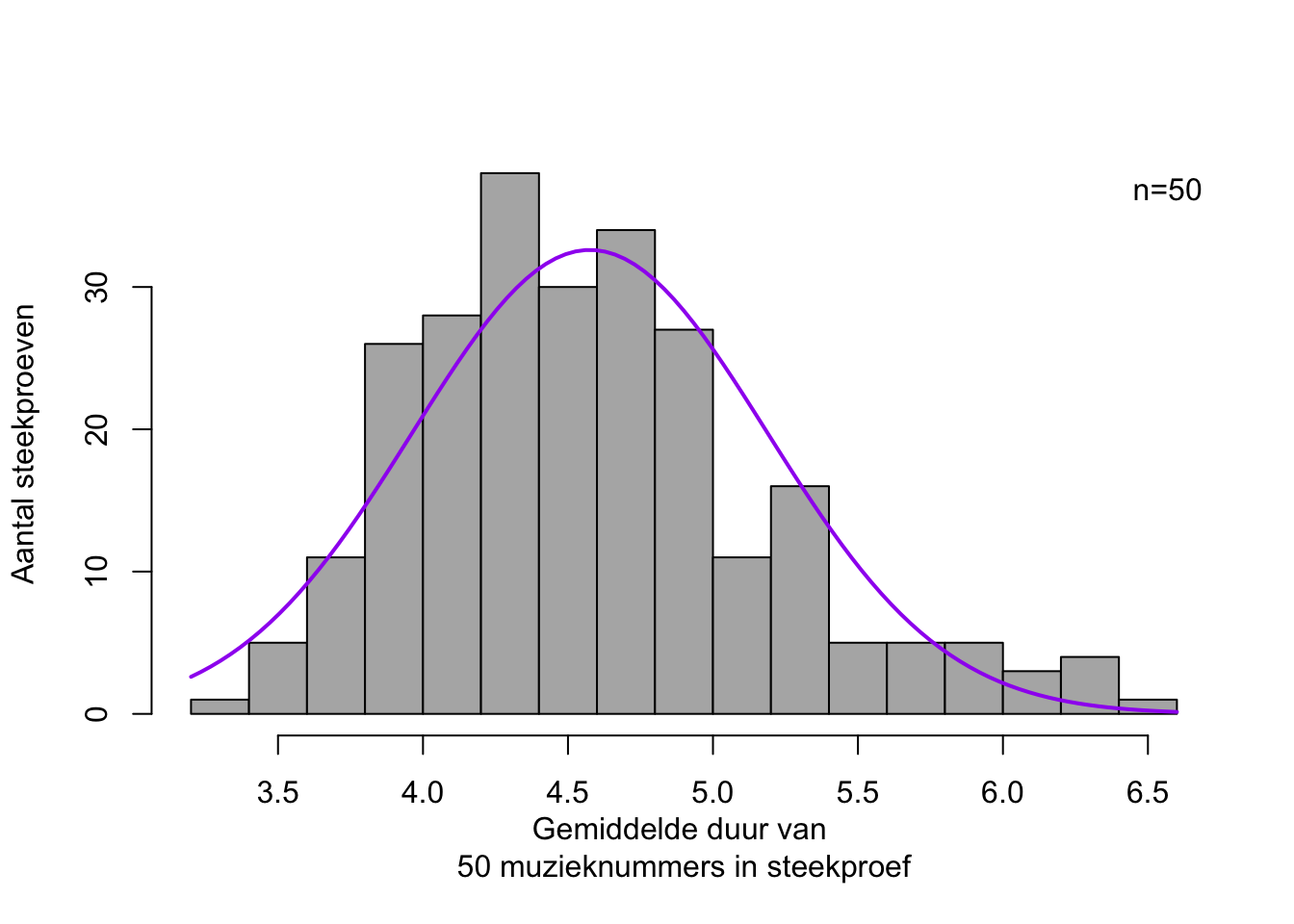
Frequentieverdeling van 250 gemiddelden, elk over een willekeurige steekproef van $n=50$ muzieknummers (de afhankelijke variabele is de duur van een muzieknummer, in minuten). De bijpassende normaalverdeling is aangegeven als een vloeiende curve.

Figuur 10.6: Frequentieverdeling van 250 gemiddelden, elk over een willekeurige steekproef van $n=50$ muzieknummers (de afhankelijke variabele is de duur van een muzieknummer, in minuten). De bijpassende normaalverdeling is aangegeven als een vloeiende curve.

Opvallend genoeg vertonen deze gemiddelden van (de afhankelijke variabele $X$ in) de steekproeven wel een min of meer normale kansverdeling, of de variabele $X$ in de populatie nu wel of niet normaal verdeeld is. Anders gezegd, de kansverdeling van een steekproefgemiddelde benadert altijd de normale kansverdeling, ongeacht de kansverdeling van de betreffende variabele in de populatie, indien tenminste de steekproef voldoende groot was. (Dit staat bekend als het Centraal Limiet Theorema). Lees de bovenstaande zinnen nog eens aandachtig door. Als vuistregel geldt dat de omvang van de steekproef, $n$, tenminste 30 moet zijn. Naarmate de steekproef groter is, wijkt de kansverdeling van de steekproefgemiddelden minder af van de normaalverdeling.

De normale kansverdeling van de steekproefgemiddelden heeft een eigen gemiddelde, $\mu_{\bar{X}}$, en een eigen standaarddeviatie, $s_{\bar{X}}$. Hiervoor geldt: \[\begin{equation} \mu_{\bar{X}} = \mu_X \tag{10.10} \end{equation}\] en \[\begin{equation} s_{\bar{X}} = \frac{s}{\sqrt{n}} \tag{10.11} \end{equation}\] De standaarddeviatie van het gemiddelde, $s_{\bar{X}}$, staat ook bekend als de ‘standard error of the mean’. De steekproefgemiddelden $\bar{X}$ hebben minder spreiding dan de afzonderlijke observaties $X$, en de gemiddelden variëren ook minder naarmate er gemiddeld is over een grotere steekproef, zoals ook blijkt uit formule (10.11). Je kunt deze standard error of the mean goed beschouwen als de ‘foutmarge’ bij de schatting van het populatiegemiddelde uit het steekproefgemiddelde.

Het bijzondere is nu, dat we niet 250 herhaalde willekeurige steekproeven hoeven te trekken en te analyseren. We weten immers dat de steekproefgemiddelden een normale kansverdeling hebben met $\mu_{\bar{X}} = \mu_X$ en $s_{\bar{X}} = \frac{s}{\sqrt{n}}$. De kansverdeling van het gemiddelde kunnen we dus afleiden uit slechts één steekproef van $n$ observaties, met één steekproefgemiddelde $\bar{X}$ en één standaarddeviatie $s$ (Cumming 2012). Lees ook deze alinea nog eens aandachtig door.

10.7 Betrouwbaarheidsinterval van het gemiddelde

Zoals hierboven uitgelegd, kunnen we het gemiddelde van de steekproef, $\bar{X}$, gebruiken als een goede schatting van het onbekende gemiddelde in de populatie, $\mu$. Op grond van het Centraal Limiet Theorema (§10.6) weten we ook dat de gemiddelden van herhaalde steekproeven (van $n$ observaties) een normale verdeling volgen: $\mu_{\bar{X}} \sim \mathcal{N}(\mu_{X},\sigma/\sqrt{n})$, en dus dat 95% van deze herhaalde steekproefgemiddelden zullen liggen tussen $\mu_{X}-1.96\sigma/\sqrt{n}$ en $\mu_{X}+1.96\sigma/\sqrt{n}$. Dit interval wordt het 95%-betrouwbaarheidsinterval genoemd. We weten met 95% betrouwbaarheid dat het populatiegemiddelde $\mu$ in dit interval ligt — mits $n$ voldoende groot is, en mits de standaarddeviatie, $\sigma$, in de populatie bekend is.

Aan die laatste voorwaarde wordt in de praktijk echter zelden of nooit voldaan. De standaarddeviatie in de populatie is doorgaans niet bekend, en deze $\sigma$ wordt daarom ook geschat uit de steekproef. We gebruiken de steekproef van $n$ observaties dus niet alleen om $\mu_X$ te schatten, maar ook om $\sigma_X$ te schatten. We mogen dan het betrouwbaarheidsinterval niet meer bepalen op grond van de standaard-normale kansverdeling. In plaats daarvan gebruiken we een aangepaste versie daarvan, de zgn. $t$-verdeling (Figuur 10.7). Deze kansverdeling van $t$ is iets breder, d.w.z. met een iets lagere top en met iets dikkere staarten, dan de standaard-normale kansverdeling van $Z$ in Figuur 10.3. De gedachte daarbij is dat de schatting van $\mu$ wat onzekerder is (dus de kansverdeling is breder) omdat niet alleen $\mu$ maar ook de standard error of the mean ($s/\sqrt{n}$) geschat wordt op grond van de steekproef. In allebei de schattingen kunnen afwijkingen zitten, waardoor iets meer kans is om een steekproefgemiddelde te vinden dat afwijkt van het populatiegemiddelde. Zoals we al zagen wordt de schatting van $\mu$ beter naarmate $n$ groter is: de $t$-verdeling benadert dan de standaard-normale kansverdeling.

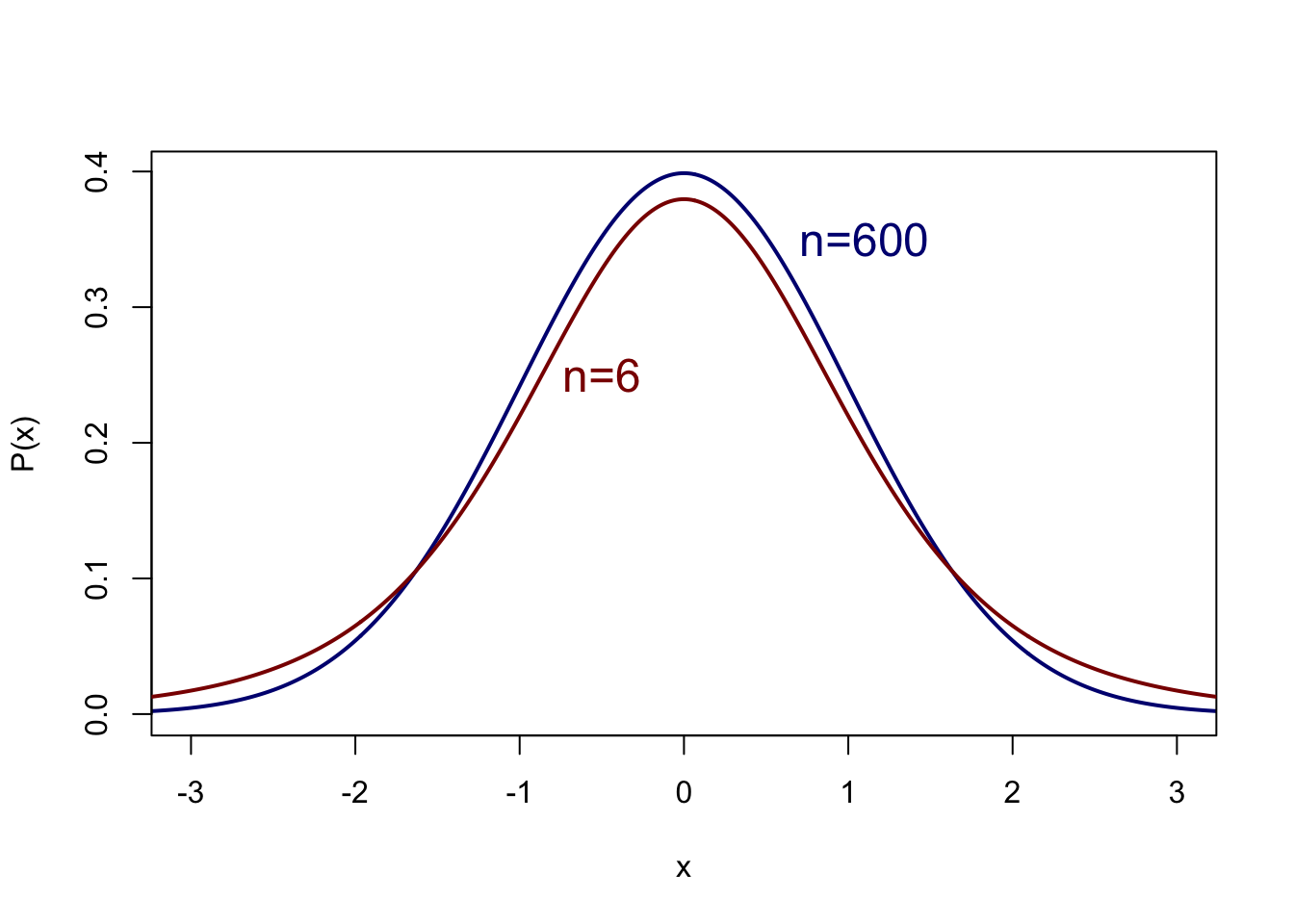
Figuur 10.7: Kansverdeling volgens de t-verdeling van een variabele $x$ met gemiddelde 0 en standaarddeviatie 1, voor n=600 en n=6.

Voor de $t$-verdeling moeten we dus weten hoe groot de steekproef was; deze $n$ bepaalt immers de precieze kansverdeling van $t$, en daarmee de kritieke waarde $t*$. We gaan daar nader op in in §13.2.1. We volstaan hier met een uitgewerkt voorbeeld.

Voorbeeld 10.11: Soms wil een onderzoeker weten hoe snel het Nederlands eigenlijk gesproken wordt, en hoe groot de variatie tussen sprekers is in deze spreeksnelheid. Deze variabele, spreeksnelheid, wordt uitgedrukt als het aantal seconden dat een lettergreep duurt (meestal $<1$ seconde). Hoewel (Quené 2008) schat dat $\mu=0.220$ s en $\sigma=0.0225$ s, doen we alsof we deze populatieparameters niet kennen — net als echte onderzoekers, die deze populatieparameters meestal ook niet kennen.

Voor een steekproef van $n=30$ sprekers vinden we $\bar{x}=0.215$ en $s=0.0203$ seconden. Daaruit schatten²² we $\hat{\mu}=0.215$ en $\hat{\sigma}=0.0203$. Omdat $\sigma$ niet bekend is, gebruiken we de $t$-verdeling om het betrouwbaarheidsinterval te bepalen. We gebruiken de $t$-verdeling voor $n=30$ en vinden een kritieke waarde $t^*=2.05$ (zie Bijlage C, voor $B=95$%). Volgens formule (10.12) weten we dan met 95% betrouwbaarheid dat het onbekende populatiegemiddelde $\mu$ ligt tussen $\bar{x}-2.05\times s_{\bar{x}}$ en $\bar{x}+2.05\times s_{\bar{x}}$, oftewel tussen $0.215-2.05\times0.0037$ en $0.215+2.05\times0.0037$, oftewel tussen $0.208$ en $0.223$ seconde Als de werkelijke waarde in de populatie tussen deze grenzen ligt, dan is er een kans van 95% om dit gemiddelde te vinden in een aselecte steekproef (Spiegelhalter 2019, 241).

In Figuur 10.8 zie je de resultaten van een computer-simulatie om dit te illustreren. We hebben $100\times$ denkbeeldige steekproeven getrokken van $n=30$ moedertaalsprekers van het Standaard Nederlands, en de spreeksnelheid vastgesteld van deze sprekers. Voor elke steekproef hebben we het 95% betrouwbaarheidsinterval getekend. Voor 95 van de 100 steekproeven valt het populatiegemiddelde $\mu=0.220$ inderdaad binnen het interval, maar voor 5 van de 100 steekproeven ten onrechte niet (deze zijn gemarkeerd langs de rechterkant).

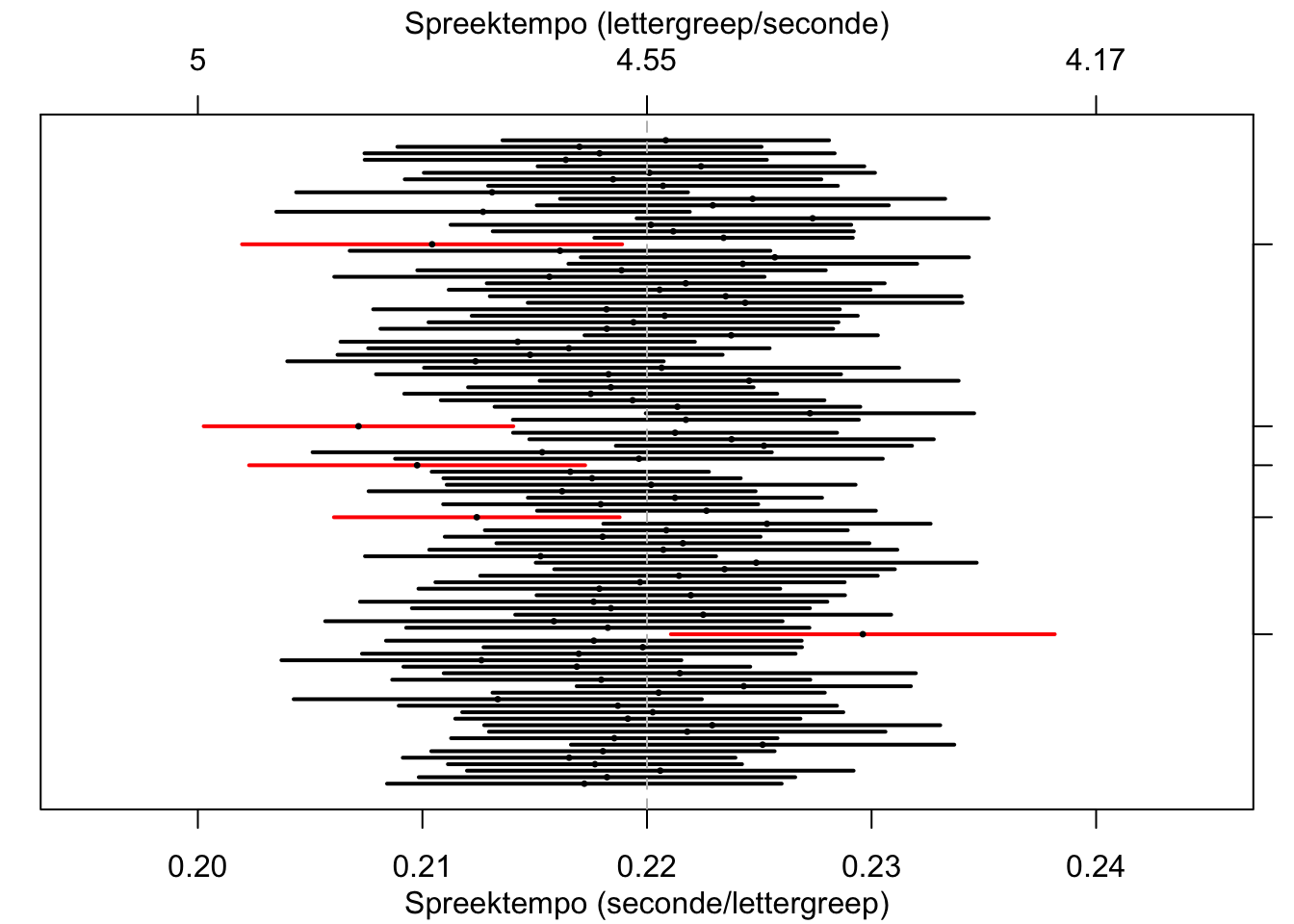
95%-Betrouwbaarheidsintervallen en steekproefgemiddelden, over 100 gesimuleerde steekproeven (n=30) uit een populatie met gemiddelde 0.220 en s.d. 0.0225; zie tekst.

Figuur 10.8: 95%-Betrouwbaarheidsintervallen en steekproefgemiddelden, over 100 gesimuleerde steekproeven (n=30) uit een populatie met gemiddelde 0.220 en s.d. 0.0225; zie tekst.

10.7.1 formules

Het tweezijdige $B$% betrouwbaarheidsinterval voor het populatie-gemiddelde is \[\begin{equation} \bar{X} \pm t^*_{n-1} \times \frac{s}{\sqrt{n}} \tag{10.12} \end{equation}\] waarbij $t^*$ met $n-1$ vrijheidsgraden gevonden wordt met behulp van Bijlage C, zie §13.2.1 voor meer uitleg hierover.

Referenties

Bhargava, Saurabh, and Vikram Pathania. 2013. “Driving Under the (Cellular) Influence.” American Economic Journal: Economic Policy 5 (3): 92–125.

Cumming, Geoff. 2012. Understanding the New Statistics. New York: Routledge.

Quené, Hugo. 2008. “Multilevel Modeling of Between-Speaker and Within-Speaker Variation in Spontaneous Speech Tempo.” Journal of the Acoustical Society of America 123 (2): 1104–13.

Schuurman, Wouter, and Hans De Kluiver. 2001. Kop of Munt: Kansrekening in Het Dagelijks Leven. Amsterdam: Bert Bakker.

Spiegelhalter, David. 2019. The Art of Statistics: Learning from Data. Pelican.

Weisstein, Eric W. 2015. “Pascal’s Formula.” Wolfram. http://mathworld.wolfram.com/PascalsFormula.html.

Twee van de fiches zijn echter zonder letter; later in deze paragraaf zullen we deze blanco fiches verwijderen uit het zakje.↩︎
Roulettespelers kunnen gokken op 36 van de 37 mogelijke uitkomsten, dus op de lange termijn ontvangt het casino $1/37$ deel van alle inzetten.↩︎
Dus ${n \choose x} = {n-1 \choose x} + {n-1 \choose x-1}$, (Weisstein 2015).↩︎
Schattingen van parameters worden aangegeven met een “dakje” erboven.↩︎

uitkomst	aantal klinkers	kans
CCC	0	\(qqq = q^3\)
VCC	1	\(pqq = pq^2\)
CVC	1	\(qpq = pq^2\)
CCV	1	\(qqp = pq^2\)
VVC	2	\(ppq = p^2q\)
VCV	2	\(pqp = p^2q\)
CVV	2	\(qpp = p^2q\)
VVV	3	\(ppp = p^3\)

aantal klinkers	kans	kans
0	\(1 q^3\)	= .2383
1	\(3 p q^2\)	= .4383
2	\(3 p^2 q\)	= .2686
3	\(1 p^3\)	= .0549
som	\((p+q)^3\)	= 1.0000

\(n= 0\):								1
\(n= 1\):							1		1
\(n= 2\):						1		2		1
\(n= 3\):					1		3		3		1
\(n= 4\):				1		4		6		4		1
\(n= 5\):			1		5		10		10		5		1
\(n= 6\):		1		6		15		20		15		6		1
\(n= 7\):	1		7		21		35		35		21		7		1